宇宙はなぜ泡のような構造をしているのか
 宇宙は約138億年前に起こったビッグバンにより誕生したと考えられています。そして現在、宇宙は数千億個ともいわれる銀河が集まった「銀河フィラメント」※1と呼ばれる領域と、銀河がほとんど存在しない「超空洞(ボイド)」と呼ばれる領域が複雑に入り組んだ、泡もしくはハチの巣のような構造をしており、「宇宙の大規模構造」や「宇宙の泡構造」と呼ばれています(図1)。
宇宙は約138億年前に起こったビッグバンにより誕生したと考えられています。そして現在、宇宙は数千億個ともいわれる銀河が集まった「銀河フィラメント」※1と呼ばれる領域と、銀河がほとんど存在しない「超空洞(ボイド)」と呼ばれる領域が複雑に入り組んだ、泡もしくはハチの巣のような構造をしており、「宇宙の大規模構造」や「宇宙の泡構造」と呼ばれています(図1)。
この構造は宇宙の歴史や成分を解明するうえで重要な情報を含んでいます。従って、宇宙の大規模構造がいつ、どのようにして形成されたかを知ることは、宇宙の成り立ちを解明する上で欠かせません。そこで、コンピュータシミュレーションを使って、宇宙の大規模構造の謎の解明に挑戦しているのが、筑波大学計算科学研究センターの田中 賢(たなか・さとし)研究員です。
宇宙の大規模構造の原因はコールドダークマター
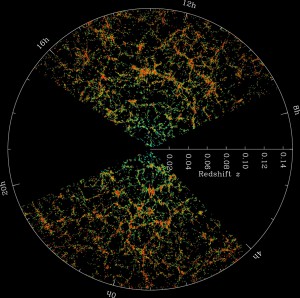
図1:宇宙の大規模構造(提供:Sloan Digital Sky Survey)
現在、宇宙の大規模構造の形成メカニズムとして最も有力なのが、宇宙が誕生した頃に起こった「密度ゆらぎ」が種となり、宇宙の膨張に伴い、大規模構造へと成長していったという説です。密度にゆらぎがあると、重力の影響で、質量がわずかに大きな領域に向かって物質がゆっくり引き寄せられ、ゆらぎが成長します。それにより重力不安定性が起こり、密度ゆらぎをさらに成長させていきます。その結果、現在のような大規模構造になったというのです。
とはいえ、銀河や恒星の主成分である水素やヘリウムだけでは重力が小さすぎるため、大規模構造を形成することはできないことがわかっています。では、密度揺らぎを作っている物質は何なのでしょうか。最新の理論によれば、それは「コールドダークマター(冷たい暗黒物質)」だと考えられています。
コールドダークマターとは、質量エネルギーに比べて運動エネルギーが小さい、言い換えると速度分散が非常に小さいダークマターです。このコールドダークマターが最初に集まり、その強い重力に引き寄せられるように、水素やヘリウムなど我々が知っている通常の物質が集まり、銀河を形成していったというわけです。
宇宙論的シミュレーションとその困難
そこで、現在、宇宙の大規模構造をコンピュータシミュレーションによって再現する「宇宙論的シミュレーション」の研究が進められています。その主流となっているのが、粒子法をベースとした「N体シミュレーション」です。粒子法とは、物質分布を“粒子”の分布として扱う数値計算手法です。これまでのN体シミュレーションによる宇宙論的シミュレーションでは、コールドダークマターを粒子として扱っていました。
一方、宇宙には大量のニュートリノが存在することが以前から知られていました。ニュートリノには質量がないと考えられていたため、宇宙の大規模構造の数値シミュレーションには考慮されてきませんでした。ところが、日本のスーパーカミオカンデによる素粒子実験により、ニュートリノはわずかながら質量を持つことが明らかになりました。ニュートリノが質量を持つならば、コールドダークマターと同様に重力が働くため、宇宙の大規模構造の形成に影響を及ぼします。
質量を持つといってもニュートリノは極めて軽いと考えられるため、速度分散が非常に大きく、宇宙の大規模構造の揺らぎの成長を抑制します。抑制の度合いはニュートリノ質量の値に依存するため、宇宙の大規模構造の観測からいまだに正確に測定できていないニュートリノの質量を求めることができると考えられています。そのため、ニュートリノの効果を取り入れた宇宙の大規模構造の数値シミュレーションが重要と考えられるようになってきました。
速度分散が非常に大きい場合、従来のN体シミュレーションでは精度よくシミュレーションできません。そこで、N体シミュレーションに代わる計算手法として田中さんが取り組んでいるのが、ニュートリノのような速度分散の大きな物質も精度よくシミュレーションする手法の開発です。
新たなシミュレーション手法の開発に挑戦
田中さんが取り組んでいるのは、「6次元位相空間上での無衝突ボルツマン方程式」を使った宇宙論的シミュレーション手法の開発です。6次元位相空間とは、座標方向3次元と、運動量方向3次元の合計6次元の位相空間のことです。
「通常のボルツマン方程式には、粒子同士の衝突による影響を加味した“衝突項”が導入されています。しかし、自己重力系の宇宙論的シミュレーションにおいては、粒子同士の衝突による影響はほとんど無視できるため、無衝突、つまり衝突項を0(ゼロ)と設定できます。この無衝突ボルツマン方程式は、『ブラソフ方程式』とも呼ばれています」と田中さん(図2)。

図2:ブラソフ(Vlasov)方程式
まず座標空間を3次元のメッシュに分割し、さらにその中に運動量空間を3次元のメッシュに分割する。分布関数fに関して、ポアソン(Poisson)方程式と組み合わせて計算する。φはポアソン方程式を満たす重力ポテンシャル(重力による質量当たりの位置エネルギー)である。
N体シミュレーションが粒子法をベースとしているのに対し、ブラソフシミュレーション(ブラソフ方程式を使ったシミュレーション)は「メッシュ法」(図3)をベースとしています。メッシュ法とは、空間をメッシュで細かく分割し、それぞれの空間の物理量を数値的に計算していく手法です。ブラソフシミュレーションであれば、広く分布する分布関数の速度成分を各メッシュに割り当てて数値計算することができるため、ニュートリノのように速度分散が大きな物質も扱えるというわけです。
しかしながら、メッシュ法の場合、シミュレーションの精度を高めるにはメッシュを細分化する必要があり、計算量や計算時間、計算に必要なメモリが膨大になるという課題があります。「例えば、6次元位相空間を扱う場合、解像度を上げて精度を高めるため、各メッシュの幅を2分の1にすると、26=64倍の計算量、計算メモリになってしまいます。そのため、近年までは、6次元位相空間の数値計算は不可能でした。しかし、スーパーコンピュータ「京」などによる大規模計算ができるようになったことで、可能になってきました。とはいえ、まだまだ計算量は膨大ですので、私はメッシュを細分化しなくても、精度を高められる手法の開発に取り組むことにしました」と田中さん。
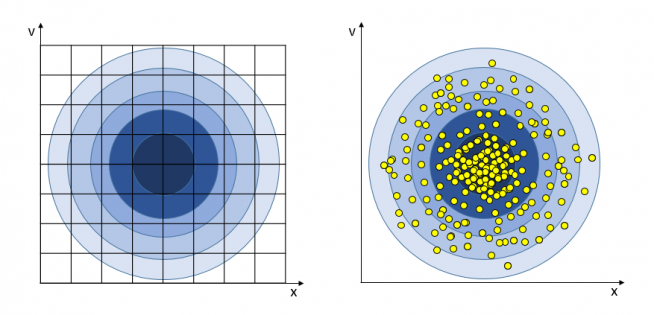
図3 : メッシュ法(左)と粒子法(右)の違い
粒子法では座標空間、速度空間からサンプリングした物理量を粒子に割り当てるため、低密度、高速度成分に割り当てられる粒子がほとんどなく、ノイズが含まれてしまう。メッシュ法では全領域の物理量の計算が可能であるが6次元計算の場合、容易にメッシュ数を増やすことができない。
N体シミュレーションとブラソフシミュレーションの違い
実は、6次元位相空間上でのブラソフシミュレーションは、2013年にすでに試みられており、それに世界で初めて成功したのが、田中さんの共同研究者である筑波大学の吉川耕司講師と、東京大学の吉田直紀教授でした。
二人は「空間3次精度のPFC法」を用いて、6次元位相空間上でのブラソフ方程式を計算していました。しかし、この手法でコールドダークマターの重力のみを考慮した宇宙論的シミュレーションを行うと、銀河団スケールなど大スケールにおいて結果が一致しなければならないはずが、N体シミュレーション結果との不一致が見られたのです。
そこで、田中さんがまず取り組んだのが、コールドダークマター計算で大スケールにおいてN体シミュレーションとブラソフシミュレーションの結果を一致させることでした。結果が一致しない原因としては、計算精度の低さが考えられました。しかし、単純にメッシュ数を増やして精度を高めようとすれば、計算量が膨大になってしまいます。そこで、田中さんが着目したのが、ブラソフ方程式を解く際に、計算が必要となる移流方程式※2の“精度”を高めることでした。空間3次精度のPFC法を使わず、空間5次精度または7次精度の正確さで計算が可能な「MP(Monotonicity Preserving)法」を採用することにしたのです。
あるメッシュの物理量の計算の際に、自身と隣り合う2つのメッシュを加え、3つのメッシュの値を扱うことで、空間3次精度でメッシュの値を更新することができます。同様に、空間5次精度では、5つのメッシュを使って値を更新、空間7次精度では、7つのメッシュを使って値を更新します。それにより、空間3次精度のときよりも高い精度で値を更新できるというわけです。「これにより、全体のメッシュ数を増やすことなく、計算精度を高めることが可能です」と田中さん。加えて、MP法に分布関数が負の値にならないようにするなど制約条件を適用しました。
その結果、座標空間1次元、運動量空間1次元の位相区間上で重力不安定性のシミュレーションを行ったところ、空間5次精度のMP法および空間7次精度のMP法を使うことにより、空間3次精度のPFC法に比べて、大幅に計算精度を改善していることがわかりました(図4)。
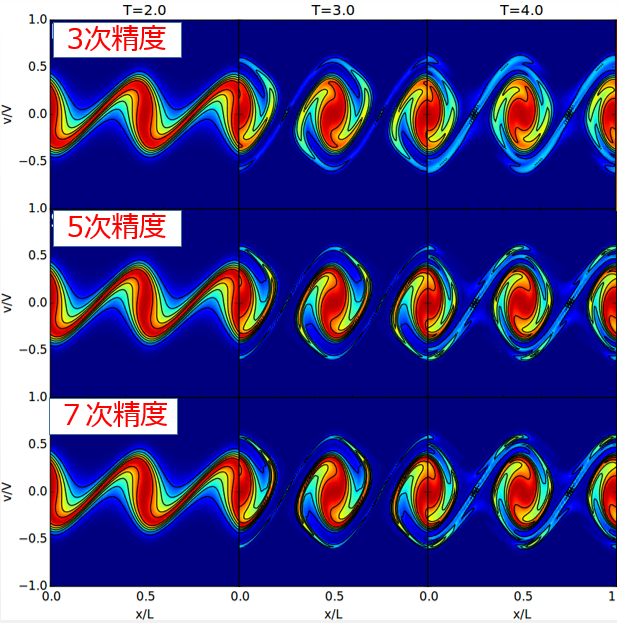
図4:重力不安定性のシミュレーション結果
空間3次精度のPFC法(1段目)、空間5次精度のMP法(2段目)および空間7次精度のMP法(3段目)を使った座標空間1次元、運動量空間1次元の位相区間上でのシミュレーション結果。精度を上げるとより細かい構造まで表現できるようになっていることを確認した。
さらに、6次元位相空間上においてコールドダークマターのみの宇宙論的シミュレーションをN体シミュレーションの結果と比較したところ、銀河団スケールでの空間3次精度で見られた値のズレが解消され、空間5次精度と7次精度では、期待される結果が得られていることを確認したのです(図5)。加えて、田中さんは「京」のプロセッサに搭載されている「SIMD命令」と呼ばれる機能を有効に活用することにより、通常に比べて約3倍の計算速度の向上を実現しました。
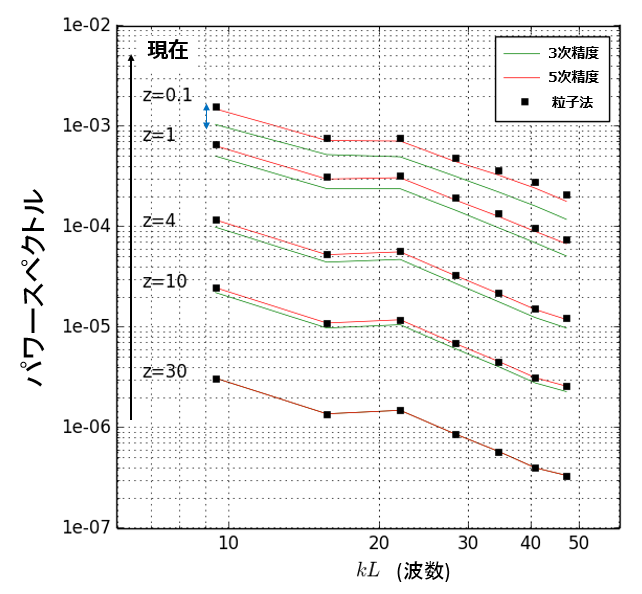
図5:コールドダークマターを対象とした宇宙論的シミュレーション結果
粒子法によるN体シミュレーション(■)、3次精度のPFC法(緑線)、5次精度のMP法(赤線)。粒子法は観測結果を良く表している。3次精度はグラフが下から上にいくに従って、粒子法に比べてずれていってしまうのに対し、5次精度は粒子法にほぼ一致していることを確認した。
2つのシミュレーションを連携させて大規模構造の解明を目指す
「この研究をやっていて、一番うれしい瞬間は、想定通りのシミュレーション結果が得られたときですね。特に、スーパーコンピュータでなければできないような大規模計算において、実際の物理現象の結果と合致したときは、自分の計算手法は間違っていなかったと確信することができ、大きな自信につながります」と田中さんは語ります。
今回の成果を基に田中さんは、本来の目的である、速度分散の大きなニュートリノを加味したブラソフシミュレーションの実行に向けて準備をしているところです。
「最終的には、N体シミュレーションとブラソフシミュレーションを連携させ、大きな速度分散を持った成分はブラソフシミュレーションを用い、速度分散が非常に小さいコールドダークマター成分はN体シミュレーションを用いた宇宙論的シミュレーションを行うことで、将来の観測との比較を目指したいと考えています」と田中さん。
さらに近い将来、ポスト「京」スーパーコンピュータが完成すれば、メッシュを細分化することによる高精度化も期待できます。ハードウエアとソフトウエアの両輪により、今後も宇宙の大規模構造の謎に迫っていきます。
用語解説
※1 銀河フィラメント
銀河がひも状に集まっているものを銀河フィラメントと呼び、フィラメント同士が交差している部分に銀河団が存在する。銀河は数百から千個程度集まって銀河団を形成し、さらに、銀河団が複数個集まり、超銀河団を形成している。
※2 移流方程式
移流(いりゅう)とは、流れに沿って物質が移動する現象のことで、これを記述したものを移流方程式と呼ぶ。ブラソフ方程式を数値的に計算する場合は、分布関数に対する移流方程式を空間方向に3本、運動量方向に3本計算することになる。














































