たった1枚のグラフを描くために、スーパーコンピュータをもってしても1年かかる。そんな大変な研究を行う筑波大学計算科学研究センター研究員の滑川裕介（なめかわ・ゆうすけ）さん。「複雑な計算はしているけれど、素粒子の基本法則はシンプルです。論理的にたどっていけば、式は1つ。そこが面白いところです」と語ります。素粒子の一つである「チャームクォーク」に関する知られざる性質を明らかにしようと、日夜シミュレーション研究にいそしんでいます。
未知がいっぱいのチャームクォーク
私たちの身の回りの物質は、原子が組み合わさってできています。その原子は、陽子と中性子からなる原子核と、電子からできています。陽子や中性子はさらに小さな「クォーク」の集合体です。いまのところ、クォークが物質の最も小さな構成要素です。クォークも何かからできている可能性は有りますが、クォークより小さい成分はまだ見つかっていません。クォークには6種類あり、質量が小さいほうから順に、アップ・ダウン・ストレンジ・チャーム・ボトム・トップとなります（図1）。
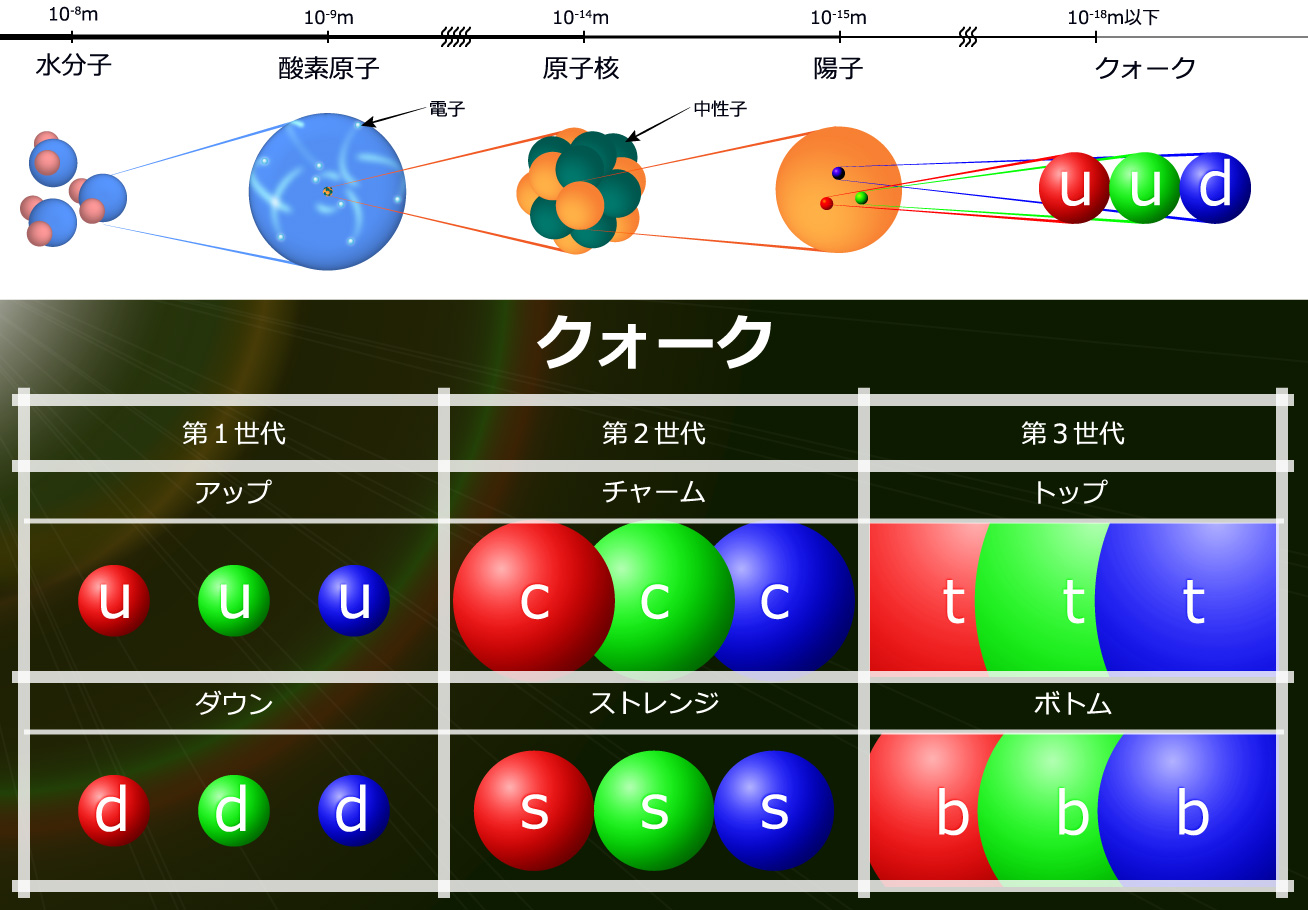
図1：物質とクォークの関係
「登山家が『そこに山があるから登る』と言うように、私は、『そこに未知があるから研究する』のです。チャームクォークには未知がいっぱい残されています」と山登りが趣味の滑川さん。未知がたくさん残されている理由は、チャームクォークの質量が中途半端だからです。質量が小さくもなく大きくもないというのは、非常に研究がしにくいのです。
軽いアップ・ダウンや重いボトム・トップに対しては近似計算法が有効なので、基本的に紙と鉛筆で計算できます。ところが、中途半端な質量のストレンジとチャームに対しては、近似計算法がうまく機能しません。一方、スーパーコンピュータを使ったシミュレーションは万能です。計算コストはかかりますが、ストレンジやチャームでも計算可能です。
真か偽か―実験結果をシミュレーションで検証する
滑川さんがシミュレーションで明らかにしたバリオンの質量について紹介しましょう。バリオンとは、クォークが3つ集まった粒子です。6種類のクォークの中から、どのクォークを組み合わせるかによって、多種多様なバリオン※1になります。
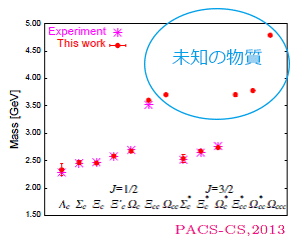
図2：バリオン質量のシミュレーション結果
滑川さんが筑波大学計算科学研究センターのスーパーコンピュータ「PACS-CS」を使用して、合計1年もの時間をかけて計算した。シミュレーションを行えば、まだ実験では捕らえられていないチャームクォーク2つや3つのバリオンの存在も予測できる。出典：Y. Namekawa et al. (PACS-CS Collab.), Physical Review D87, 094512 (2013)
滑川さんは、チャームクォークを含むバリオンの質量をコンピュータシミュレーションで計算しました（図2）。ピンクの星印は実験で観測されたバリオンの質量、赤丸が滑川さんのシミュレーション結果です。赤丸のみが示されているバリオンは、まだ実験で観測できていない、未知のバリオンです。滑川さんはシミュレーションで、「この質量を持ったバリオンがこの世の中には存在するだろう」という予測をしました。現在、世界中の実験研究をするチームが、これらのバリオンを検出しようとしのぎを削っています。
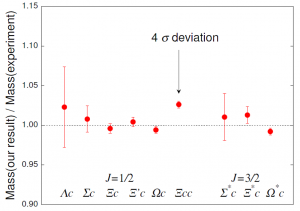
図3：バリオン質量シミュレーション結果を実測結果で割った値
赤丸の上下に伸びる赤い棒は誤差範囲。滑川さんが行うシミュレーションでは、計算を始めて2～3カ月の頃は誤差範囲が広く、実験結果が正しいかどうかはわからなかった。データを積算していくうちに、誤差範囲がだんだん狭まっていく。1年近く積算した結果、他のバリオンは実験結果に近いのに、Ξccだけが実験結果から外れていく様子をみた滑川さんは「まず我が目を疑い、次に自分のプログラムに間違いが無いか疑い、胃が痛くなりそうになりながら計算に不備がないか何度も確認しました。しかし、問題は見つからず。最終的に、この実験結果は正しくない可能性が高いと判断しました」。
実は図2は、論争になっているある実験データに1つの「ダメ出し」証拠を突きつけてもいます。チャームクォーク2つを含むバリオンの観測は、世界でただ1チームだけが成功したとして報告しています。それが図2に示したダブルチャームグザイバリオン（Ξcc）の星印です。他にも世界で3チームが観測に挑戦していますが、まだ成功していません。これら3チームは「この観測値は間違っているのではないか」と主張しています。
滑川さんのシミュレーション結果は、真か偽かという問いに「偽」という判断材料を提供しています。そして、「もう少し大きい質量を狙って観測すれば見つかるはずだ」というメッセージも提供しています。
図3は、滑川さんのシミュレーションから算出した質量を、実験結果で割った値を示しています。シミュレーション結果と観測結果が一致していれば、ちょうど1になります。論争になっているデータは黒矢印をつけたΞccです。他のバリオンは誤差範囲を考慮すれば1に近いのに、Ξccだけが、誤差範囲の約4倍も1から外れてしまっています。どうも実験結果が間違っている可能性が高そうです。シミュレーションは、より大きなΞccの質量値を示しています。
直接実験できないときこそ、シミュレーションの出番
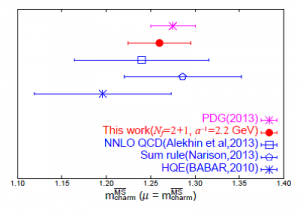
素粒子の世界には、実験ではどうしても観測できない値があります。それを求めるのもシミュレーションが得意とするところです。たとえば、チャームクォークの質量（図4）が挙げられます。クォークは単独で存在できず、その質量を実験観測で決定することは物理的に不可能です。しかし、シミュレーションを駆使すれば、クォーク質量などの直接観測できない量すら決定できます。
図4：チャームクォーク質量値の比較
様々な研究グループが算出したチャームクォークの質量値。PDGは世界中の結果から毎年割り出される世界標準値。赤丸が滑川さんのシミュレーション結果。出典：Y. Namekawa et al. (PACS-CS Collab.), Phys. Rev. D84, 074505 (2011)
シミュレーションの工夫と努力
図5：格子QCDのイメージ図
4次元時空を格子間隔aで分割(離散化)することで、シミュレーションが可能になる。
「チャームクォークのシミュレーションは、アップ・ダウン・ストレンジクォークの場合と違い、一筋縄ではいきません」と滑川さんは言います。そんな中でも、「私たちの研究は精確な値になるよう工夫しています」と滑川さんは自信をのぞかせます。いったい、どのような工夫をしたのでしょうか。
滑川さんは「格子量子色力学（こうし りょうしいろりきがく）」という手法を使っています。クォーク及びクォークの間に生じる強い力の理論である量子色力学（QCD、Quantum ChromoDynamicsの略）を格子上で定式化し、シミュレーションを可能にした計算方法です（図5および月刊JICFuS第3号2段落目「QCD」はクォークとグルーオンの力学 を参照）。
この格子が粗い（格子間隔aが大きい）と非連続の世界となり、現実から遠のいて（離散化誤差が入って）しまいます。ですから、格子間隔aをなるべく小さく設定したいのですが、そうすると計算量は莫大になってしまいます。そこで滑川さんは、計算式の中で格子は粗くとりながらも、離散化誤差が小さくなる工夫をしています（図6）。
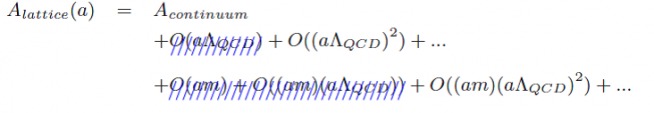
図6：格子QCDでの計算の工夫
Ａlattice(a)は格子QCDで求めた物理量、Acontinuumは物理量の真の値、Ｏ（ ）は離散化誤差を表す。誤差の値が大きくなる青斜線を付した項が消えるように計算の工夫をしている。aは格子間隔で、ΛQCDは定数。通常、（aΛQCD）は１より小さい値。aが1乗で効くＯ（aΛQCD）は大きな誤差となる。Ｏ（am）とＯ（（am）(aΛQCD)）にはチャームクォークの質量ｍが入る。チャームクォークのシミュレーションではｍが大きい値となるので、この項も大きな誤差として結果に悪影響を及ぼしてしまう。
これらの誤差を消す工夫をすることで、ある程度大きな格子間隔aを使っても誤差が小さい計算となり、比較的少ない計算量でも精確なシミュレーションができるようになった。
この工夫で、100倍から1000倍効率の良い計算ができるようになりました。これは、100年～1000年かかる計算が1年に短縮できたことを意味します。
計算機への指令書ともいうべき計算コード※2は実に8万行。うまく計算が動くようになるまでに悪戦苦闘がありました。どこが原因で動かないのかを根を詰めて考えていると、“夢のお告げ”があったことも。夢から覚めてコンピュータに向かうと、本当にお告げの箇所にエラーを発見したという経験が何度もあるそうです。
未知はたくさん残っている
クォークに働く「強い力」のみを考慮した研究を中心に紹介してきましたが、滑川さんは、残り3つの相互作用「電磁気力」「弱い力」「重力」も計算に取り入れたいと考えています。強い力に加え上記3つの力を含めることで、本当の意味で現実世界をシミュレートできるためです。すでに、電磁気力を取り入れたより現実的なシミュレーションを行っています。ただ、弱い力や重力は、どうやって格子上の計算式にすればよいのかすらわかっていないのが現状だそうです。研究すべき未知はたくさん残っています。
用語解説
- 1 多種多様なバリオン
- たとえば、アップ・ダウン・チャームの各クォークが1つずつ組み合わさるとチャームラムダバリオン（Λc）、アップクォーク1つとチャームクォーク2つが組み合わさるとダブルチャームグザイバリオン（Ξcc++）となる。
- 2 計算コード
- 使用するコードはBridge++。滑川さんもBridge++の中心開発メンバーの一人である。くわしくは、月刊JICFuS「シミュレーション手法の共通化でクォークの謎の解明に貢献」（2015年1月）を参照。
