ニュートリノの性質を明らかにすることは、宇宙や星の成り立ちの解明につながります。「究極の目標は、われわれの世界はどうできているのかを明らかにすること」と話すのは東京大学大学院理学系研究科附属原子核科学研究センター特任助教の岩田順敬(いわた・よりたか)さんです。岩田さんは、殻模型※1という原子核の構造を記述するモデルを使って、ニュートリノの謎を解く鍵となる「原子核の二重ベータ崩壊」の過程を計算で明らかにしようとしています。
ニュートリノの性質を明らかにすることは、宇宙や星の成り立ちの解明につながります。「究極の目標は、われわれの世界はどうできているのかを明らかにすること」と話すのは東京大学大学院理学系研究科附属原子核科学研究センター特任助教の岩田順敬(いわた・よりたか)さんです。岩田さんは、殻模型※1という原子核の構造を記述するモデルを使って、ニュートリノの謎を解く鍵となる「原子核の二重ベータ崩壊」の過程を計算で明らかにしようとしています。
宇宙と物質の謎を解く
ニュートリノは電荷を持たず、質量が非常に小さい素粒子です。他の物質とほとんど反応せず、検出が難しいため、その性質には多くの謎が残されています。中でも重要なのは、質量の値と、ニュートリノがマヨラナ粒子であるかどうかの2つです。
1つめのニュートリノの質量は、はじめはゼロと考えられていました。1998年にスーパーカミオカンデの実験によって質量が“ある”ことが発見されましたが、その値がまだわかっていません。
2つ目のマヨラナ粒子※2は、粒子と反粒子が同じという性質を持った理論上の物質です。通常は、陽子(+)と反陽子(-)のように電荷が違うため、粒子と反粒子は異なります。マヨナラ粒子はいまだに発見されておらず、その有力候補とされるのがニュートリノなのです。
ニュートリノがマヨラナ粒子であるかどうかを明らかにすることは、宇宙の物質生成の解明につながります。現在の宇宙には反粒子が存在しません。その理由は、宇宙が誕生したころには粒子と反粒子が大量に存在していたものの、粒子が反粒子より100億分の1だけ多かったため、同数の粒子と反粒子が対消滅して光(エネルギー)に変わった後に、粒子だけが残ったからだと考えられています。この100億分の1の違いを、ニュートリノがマヨラナ粒子であれば、自然に説明できるのです。
質量はいくらなのか、マヨラナ粒子か否か。「ニュートリノの謎を解くために、私たちは二重ベータ崩壊過程を計算で明らかにしようとしています」と岩田さんは話します。
謎解きの鍵を握る二重ベータ崩壊
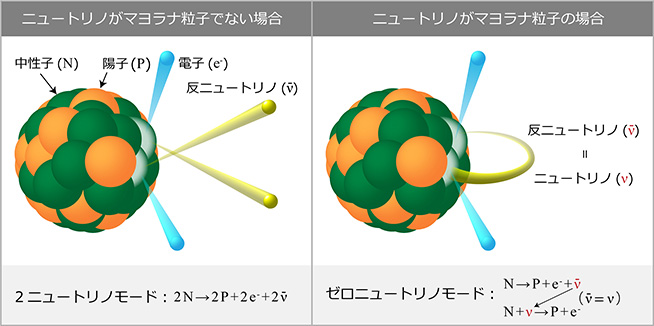
図1:二重ベータ崩壊
ニュートリノがマヨラナ粒子なら、48Caはゼロニュートリノモードを引き起こす可能性がある
ベータ崩壊とは、原子核中の中性子が陽子に変化し、弱い相互作用によって電子や反ニュートリノが放出される現象です。ベータ崩壊が同時に起こる二重ベータ崩壊には2つのモードがあります(図1)。2個のニュートリノが放出される2ニュートリノモード(2ニュートリノ二重ベータ崩壊)と、ニュートリノが放出されないゼロニュートリノモード(ゼロニュートリノ二重ベータ崩壊)です。
ゼロニュートリノ二重ベータ崩壊が見つかれば、ニュートリノはマヨラナ粒子であることを証明できます。マヨラナ粒子ならばニュートリノと反ニュートリノが同一であるため、ニュートリノが現れないゼロニュートリノ二重ベータ崩壊が起きるからです。さらに、その半減期からニュートリノの質量を求めることができます(図2上)。
今、世界中でゼロニュートリノ二重ベータ崩壊を明らかにしようと実験が行われています。しかし、半減期からニュートリノの質量を求めるために必要な核行列要素は、実験から直接求めることができません。また、核行列要素はゼロニュートリノ二重ベータ崩壊の起こりやすさの指標ともなります。そのため、核行列要素を高い精度で計算する必要があるのです。
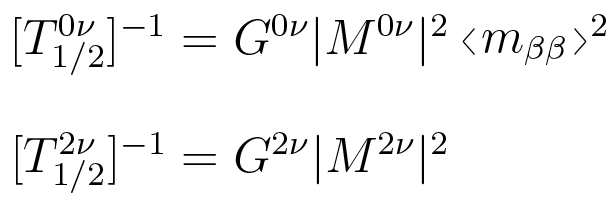
図2:ゼロニュートリノ二重ベータ崩壊の崩壊率(上)と2ニュートリノ二重ベータ崩壊の崩壊率(下)を表す公式。
T1/2は半減期、Mは核行列要素、mββはニュートリノの有効質量。また、Gは位相空間因子。
二重ベータ崩壊の核行列要素を求める
岩田さんたちは、ゼロニュートリノ二重ベータ崩壊の核行列要素を求めることを目指しています。まずは実験により崩壊寿命が知られている48Ca(カルシウム)の2ニュートリノ二重ベータ崩壊の核行列要素を求めることにしました(図2下)。これまで、10種類ほどの原子核で2ニュートリノ二重ベータ崩壊が実験的に観測されています。それらの原子核のうち、48Caは最も軽い原子核で、半減期が一番短いことや放出エネルギーが大きいことから、ゼロニュートリノ二重ベータ崩壊の探索の有力な候補です。
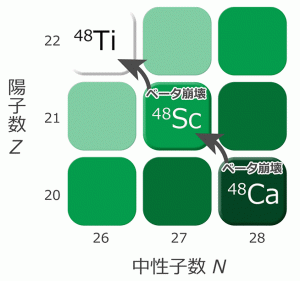
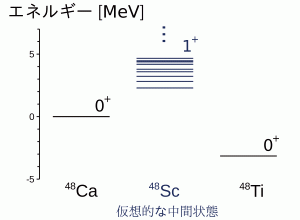
二重ベータ崩壊では、原子核内の2つの中性子がほぼ同時に陽子になりますが、原子核が2回連続してベータ崩壊すると仮定すると、48Caは仮想的な中間状態である48Sc(スカンジウム)を経て、48Ti(チタン)になります(図3)。このとき、ガモフ・テラー遷移とよばれる遷移が起こります。48Caの基底状態(0+)は、48Scの1+状態よりもエネルギー的に安定です(図4)。そのため、48Caが48Scにベータ崩壊することはありません。二重ベータ崩壊を考える際には、48Scの1+状態は仮想的な中間状態として扱われ、すべての1+状態を考慮に入れる必要があります。中間状態を精密に記述するためには、より大きな模型空間を考えて、陽子や中性子の相互作用を扱わなければならないのです。
「ゼロニュートリノ二重ベータ崩壊では、強い相互作用と弱い相互作用が密接にはたらいています。2ニュートリノ二重ベータ崩壊の核行列要素を大きな模型空間で計算して実験結果と比較することで、ゼロニュートリノ二重ベータ崩壊の研究には欠かせない、より正確な波動関数と強い相互作用を得たいと考えています」と岩田さん。
殻模型の模型空間を広げる
これまで行われてきた計算では、48Scの高エネルギー状態へのガモフ・テラー遷移強度が十分に再現されていませんでした。そこで岩田さんたちは、大規模な殻模型計算により核行列要素を求めることにしました。
原子核の中で陽子や中性子は、お互いに引っぱったり反発したりしながらいろいろな軌道を動き回っています。殻模型計算では、陽子数または中性子数が特定の数であるときに閉殻が形成されるという殻構造を仮定したうえで、相互作用する陽子や中性子の運動を計算します。
これまで行われてきた計算では、殻模型の模型空間を1つ(1主殻)とったものでした。しかし、1主殻の48Caの計算では陽子が動かず、異なる主殻をまたいで起こる核子励起を無視してしまうことになり、高励起状態を記述できないなどの問題がありました。そこで岩田さんたちは、模型空間を2主殻に増やし計算することにしました。模型空間を広げると自由に動くことができる粒子の数が増え、粒子の動きやエネルギー準位をより詳細にとらえることができます。しかし、模型空間を増やすと計算はきわめて困難となり、莫大な計算量になります。計算には行列の対角化が必要ですが、対角化しなければならない行列の次元が100億を超えます。これはスーパーコンピュータ「京」を使ってもぎりぎり計算できるかどうかです。
大規模殻模型計算ではモンテカルロ法(乱数を用いた手法)が使われることもありますが、48Caの場合、核内での妥当な相互作用がわかっていないので、たくさんの条件が必要なモンテカルロ法は適していません。そこで、岩田さんたちは、ランチョス法による厳密対角化を使いました。ランチョス法は、出てきた行列を直接対角化する方法です。初期状態や終状態、中間状態を計算する際に可能な励起に制限を設けることで、行列の次元を100億から7億ほどに減らすことができました。
計算機の進歩が殻模型の可能性を広げた
実験では、48Caの第二0+状態には陽子励起を含んでいると指摘されていますが、これまでの1主殻の計算ではその状態を含むことはできませんでした。今回は、2つの殻の相互作用を検討し、励起エネルギー状態を再現するよう相互作用をつくりました。この相互作用を用いて計算すれば、48Caや48Tiの基底状態にも、陽子や中性子などの励起成分が混ざります。そうして得られた核行列要素を、これまでの1主殻計算や実験値と比較しました。2主殻計算では、エネルギー遷移状態をうまく記述することができました。
「2主殻の殻模型を使って、精度の高い計算ができるようになったのも、計算機の技術が進歩のおかげです」と岩田さん。これまでの殻模型計算では計算できる模型空間が限られていて、信頼性の高い結果を得ることが難しかったのです。近年の計算機の目覚ましい発展により、殻模型の計算空間は広がりました。今後、殻模型計算はあらゆる原子核に応用できると期待されています。
岩田さんたちは、2主殻での計算によって、ニュートリノの謎の解明に迫っています。「より精度の高い核行列要素を求めることは、計算でしかできません。そのためには殻模型計算は重要なツールです。大規模殻模型計算によって、ゼロニュートリノ二重ベータ崩壊のプロセスを解明したいです」。
用語解説
- 1 殻模型
- 殻とは、原子核内が『殻』のような構造をもっているのではなく、陽子や中性子の数が特定の数(2、8、20、28、…)をとったときに全体として特に安定になることを意味する。たとえば48Ti(陽子22、中性子26)の場合、陽子20個、中性子20個で極めて安定な“閉殻”ができると考える。閉殻は安定なため動かないものとし、残りの陽子2個、中性子6個を扱った8体問題を完全に解くのが殻模型計算の考え方である。1主核計算は陽子20個、中性子20個を閉殻に取り、2主殻計算は陽子8個、中性子8個を閉殻に取ることを指す。2主殻計算では32体問題を考えることになる。
- 2 マヨナラ粒子
- 素粒子は、電荷の正負のほか、スピンが半整数(1/2)か整数(0)かによって性質が大きく異なる。スピン半整数をフェルミ粒子、スピン整数をボース粒子と呼び、フェルミ粒子のうち電荷をもつものをディラック粒子、電荷をもたないものをマヨナラ粒子と呼ぶ。マヨラナ粒子はいまだに発見されておらず、電荷を持たないニュートリノはマヨナラ粒子の有力候補とされる。