格子QCDで原子核を解明する－クォークとグルーオンから原子核を形成する力を導けるのか

2つの陽子と2つの中性子－4つの核子からなるヘリウム原子核。名古屋大学素粒子宇宙起源研究機構の山﨑剛（やまざき・たけし）特任助教は、これを「多体核子」と表現します。核子が4つで「多体」とは少ないように思うかもしれません。しかし、核子ひとつひとつは、物質を構成する最小単位と考えられている素粒子、クォーク3つとグルーオンで構成されています。素粒子の振舞いから原子核の性質を計算する山﨑さんにとって、ヘリウム原子核は4核子の集合体ではなく、その数倍の素粒子が複雑に影響を及ぼしあっている集団に見えているのです。2009年には、「こんな複雑な計算はまず無理」と考えられていました。それを可能にした山﨑さんは、どのような工夫を重ねてきたのでしょうか。

素粒子からヘリウム原子核を計算する

山﨑さんが挑んでいるのは、「格子QCDを使ってヘリウム原子核の束縛状態を計算で確かめる」という研究です。
格子QCD（Quantum Chromo Dynamics：量子色力学）とは、素粒子のうちクォークとグルーオンに働く「強い力」を計算可能にした理論です（くわしくは月刊JICFuS第3号2段落目「QCD」はクォークとグルーオンの力学を参照）。格子の交点にクォークを、点を結ぶ辺にグルーオンを配置することで、素粒子間に働く力の計算をしていきます（図1）。

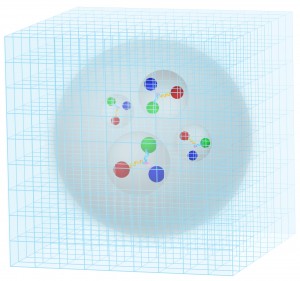
図1：格子QCDのイメージ図
計算の便宜上、クォークとグルーオンを格子状に配置する。格子のサイズを無限大にすると格子という型にはめ込んだ影響がなくなり、実際の状態に近づけることができる。素粒子に働く4つの力（重力、弱い力、電磁力、強い力）のうちの「強い力」について計算ができる。

束縛状態とは、原子核を作る素粒子がそれぞれ独立して散らばっているのではなく、原子核としてぎゅっとかたまりを形成している状態のこと。つまり、格子QCDで計算した核子のエネルギーとヘリウム原子核のエネルギーを比較して「束縛状態である」という結果になれば、計算に使った素粒子は原子核という集団として安定に存在すると考えられます。

なぜ、山﨑さんは「格子QCDを使ってヘリウム原子核が束縛状態を形成するか」に興味を持ったのでしょうか。
ノーベル物理学賞を受賞した湯川秀樹博士は、陽子と中性子を強く束縛し、原子核を形成するための力のもととなるパイ中間子の存在を1935年に提案しました。後に、パイ中間子が確かに存在すると実験で確かめられました。
ところが、今は、クォークとグルーオンが陽子や中性子を作っていると考えられるようになりました（図2）。そこで、パイ中間子ではなく、素粒子に働く力から原子核を束縛している力を説明してみようと山﨑さんは考えたのです。
ヘリウムは最も安定な原子核として知られています。安定とは、束縛のエネルギーが大きいということです。そのため山﨑さんは、他の原子核よりも容易に束縛エネルギーが計算できるだろうと考えました。

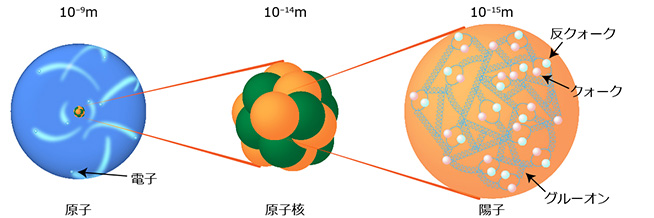
図2：クォークとグルーオンの模式図
原子核は陽子と中性子からできており、陽子はuudという二種類3個のクォークとその力を媒介するグルーオンからなる。中性子は、uddとグルーオンからなる。クォークとグルーオンは現在、物質を構成するもっとも小さい単位と考えられている。uはアップクォーク、dはダウンクォークを表す。

3つの難しさ

山﨑さんがこの研究を始めた2009年当時、ヘリウム原子核について格子QCDで計算する研究者は誰もいませんでした。というのも、この研究には3つの課題があったからです。

第1は誤差の問題です。この研究で使う計算式に含まれる誤差は、核子数が増えると指数関数的に大きくなってしまうというものでした。ヘリウム原子核の核子数は4つ。数値計算にとって「特別に悪い振る舞いをする」誤差だったのです。

第2の問題は計算コスト（計算量）です。格子QCDで素粒子間に働く力を計算する場合、核子を構成単位とするときよりはるかに多くの粒子間相互作用を計算しなければなりません。計算量の指標となるクォーク縮約数^※1は、核子1つであれば2であるのに対し、核子が4つのヘリウム原子核（⁴₂He）の場合は518,400と桁違い。Lattice2009国際会議^※2の基調講演で「核子数が4の計算は膨大な計算時間のため実行不可能」と言及されるほど、当時としては大変な計算量だったのです。

第3の問題は、有限体積上束縛状態識別です。格子QCDの方法では、計算量を抑えるために、「クォークは限定した体積のなかに存在する」という仮定を強いられます。現実とは異なる限られた体積の範囲での計算から「束縛状態にある」という結果が得られたとしても、それが有限体積にクォークを押し込めてしまったために起こっている束縛なのか、それとも本当に原子核をつくっている束縛状態なのかを判断できないのです。

問題を乗り越えたブレークスルー

2010年、山﨑さんたちは3つの問題を乗り越える重要な発明をしました。計算量を減らす手立てを見出したのです。クォーク縮約の計算は、同じような計算を何回もしています。山﨑さんらは、分別して同じ計算を省くようにしたのです。この工夫で、518,400だったクォーク縮約数は1107にまで減りました^※3。これは、第2の問題を解決すると同時に、第1、第3の問題も解決してくれました。

第1の問題―統計誤差は、多くの測定点について計算をすることである程度減らすことができます。1つの計算にかかるコストが減ることで、多くの測定点について計算することが可能になりました。また、誤差を減らすために現実より重いクォーク質量を計算に使う^※4という方針も選択しました。
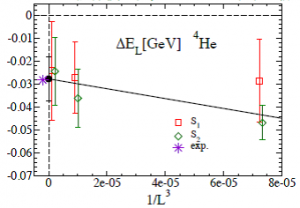
第3の問題―有限体積については、いくつかの体積についての計算を行い、無限体積へ外挿しました（図3）。その結果、無限体積での束縛状態を予測できるようになりました。1つの計算にかかるコストを減らすことができたために可能になった方法です。

このようにして山﨑さんは、ヘリウム原子核の束縛状態を計算することに成功しました（図3）。山﨑さんの計算からは、実験値に近い束縛エネルギーが算出されました。

図3：ヘリウム原子核の束縛状態計算結果
縦軸⊿Ｅが負の値をとると、原子核は束縛状態であることを示す。横軸は計算に使った体積の逆数。この図では、3つの異なる体積について計算して外挿直線を算出。外挿直線が縦軸と交わる点（体積が無限大での束縛エネルギー）を予測した。青星印は実測値を表す。S1とS2は2種の異なるパラメータを用いた計算で、これらが近い値となったことで、計算が確からしいということがわかった。

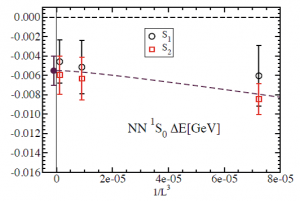
図4：現実には存在しない核子2つの束縛状態計算結果
陽子と陽子、あるいは、中性子と中性子の束縛状態を計算した結果。現実には存在しない原子核なので原点を通るグラフになるはずが、横軸が0のときに負の値を示している。

ところが、山﨑さんは「この結果は大喜びというわけにいかない」と言います。なぜなら、同じ手法で、現実には存在しないはずの陽子二つだけ、あるいは、中性子二つだけの場合を計算しても「束縛状態にある」という結果が出てきてしまったからです（図4）。本来なら、現実に原子核として存在しない場合は、「束縛状態はない」という結果になるはずなのです。

これは、計算量を抑えるために、実際よりも非常に重いクォーク質量を使っているからだと山﨑さんは考えています。高い計算能力をもつスーパーコンピュータ「京」を使えば、現実のクォーク質量を使った計算も可能となります。山﨑さんは2014年度からスーパーコンピュータ「京」を使った研究を始める予定です。

まだまだ欲しい計算資源

山﨑さんは、これから研究してみたいことを語るのに、「いつになるかわかりませんが、」という前置きをします。というのも、山﨑さんは計算を始めてから結果得るまでに数カ月はかかるという、とても時間のかかる計算をしているからです。図3のグラフ1つ仕上げるのに、ほぼ1年の月日を要しました。山﨑さんは「リターンキーを押したら、瞬時に答えが出てくるコンピュータがあったら良いのに」とよく考えるそうです。

コンピュータの性能が上がれば、さまざまな研究が現実的な計算時間で可能になってきます。現在、アップクォークとダウンクォークの質量は同じと近似しているので、質量の違いを考慮した研究にも挑みたいそうです。また、不安定でなかなか現実には存在しないような原子核や、もっと大きな原子核についても計算してみたいそうです。
このように研究が進んでいくと、「もしもクォークの質量が現在と少し違っていたら、この世の中はどのような元素でつくられていたのか」という研究もできると山﨑さんは考えています。