現在の宇宙はほぼ粒子からなり、反粒子はごくわずかしか存在しません。その理由は「CP対称性の破れ」にあると考えられていますが、粒子が圧倒的に多い現状を説明するにはさらなる研究が必要です。その１つとして「ニュートリノ振動」の観測が行われています。しかし、観測データを解析するには、検出器内でニュートリノが原子核に衝突したときの相互作用のシミュレーションが必要です。なかでも、核子（陽子または中性子）の形状の精密なシミュレーションを成功させたのが高エネルギー加速器研究機構（KEK）の学振特別研究員である辻竜太朗さんの研究グループです。
ニュートリノを使った実験
宇宙がビッグバンによって生まれたとき、粒子と反粒子は同数つくられたと考えられています。しかし、現在の宇宙は粒子がほとんどで反粒子はわずかしかありません。その理由は粒子と反粒子の間に「CP対称性の破れ」があるからだとされています。CP対称性とは、粒子と反粒子を入れ替えて左右を鏡に映したように反転させても、物理法則は同じはずだという考え方です。
物質をつくっている素粒子にはクォーク（陽子や中性子をつくる素粒子）とレプトン（電子やニュートリノ）の2種類があります。実験により、クォークの振る舞いにおいてCP対称性がわずかに破れていることが確認され、理論的な説明もなされています。これを「クォークセクターのCP対称性の破れ」と呼びますが、実験と理論から予想される破れの大きさは、現在の宇宙がほぼ粒子からなっていることを説明するには不十分です。このような中、「レプトンセクターのCP対称性の破れ」が起きている場合、その破れがどの程度あるのかが注目されています。
特に、ニュートリノという非常に軽いレプトンの種類が変わる「ニュートリノ振動」において、CP対称性の破れが起きている可能性があるため、それがどの程度破れているかの観測を目的とする「ニュートリノ振動実験」が行われています。日本の「T2K」、アメリカの「DUNE」はその代表例です。T2Kは、茨城県那珂郡東海村のJ-PARC加速器で人工ニュートリノビームを発生させ、岐阜県飛騨市神岡町にあるスーパーカミオカンデでニュートリノを検出する実験です。
ニュートリノという素粒子には、電子、ミューオン、タウの3種類があり、宇宙線や太陽、加速器などから大量に発生しています。ニュートリノは飛んでいる途中で、たとえば、ミューオンニュートリノから電子ニュートリノへといった具合に、種類が変化します。この現象をニュートリノ振動と呼びます。この変化する確率を調べる実験がニュートリノ振動実験です。
この確率を調べることで、CP対称性の破れの有無を確認できることが期待されています。たとえば、ミューオンニュートリノが電子ニュートリノに変わる確率と反ミューオンニュートリノが反電子ニュートリノに変わる確率を比べたとき、そこに差があることがわかれば、CP対称性の破れの謎を解く手がかりになります。
ただし、ニュートリノのフラックス（流量）を直接観測するのは難しいため、T2Kなどの実験では、ニュートリノと検出器内の原子の原子核との相互作用の頻度を観測しています。この観測量から検出器に入ったニュートリノのフラックスを導くには、ニュートリノが核子に衝突する確率（散乱断面積）が必要となります（図１）。そこで、散乱断面積を求めるため、ニュートリノを原子核や核子（陽子または中性子）に衝突させる実験や、そのシミュレーションが長く行われていますが、原子核も核子も構造が非常に複雑なため、散乱断面積を表すモデルには大きな「不定性」が含まれており、精度の高い値はまだ得られていません。
この不定性の低減を目指して、辻さんたちの研究グループは、スーパーコンピュータ「富岳」を使ったシミュレーションに取り組んでいます。シミュレーションでニュートリノが核子によって散乱されるときの高精度の散乱断面積を求めることができれば、ニュートリノ振動実験の信頼性を高め、CP対称性の破れを精密に測るための基盤となります。また、散乱断面積を求めることは、ニュートリノで核子を「見る」ことでもあるため、核子の複雑な構造の理解などにもつながると期待されます。
図1：ニュートリノ振動実験の観測データの解析では、ニュートリノの核子による散乱断面積（式の赤線部分）の精密な値が必要となる。辻さんたちは、そのシミュレーションに取り組んでいる。
最も大きな不定性をもつ「軸性形状因子」
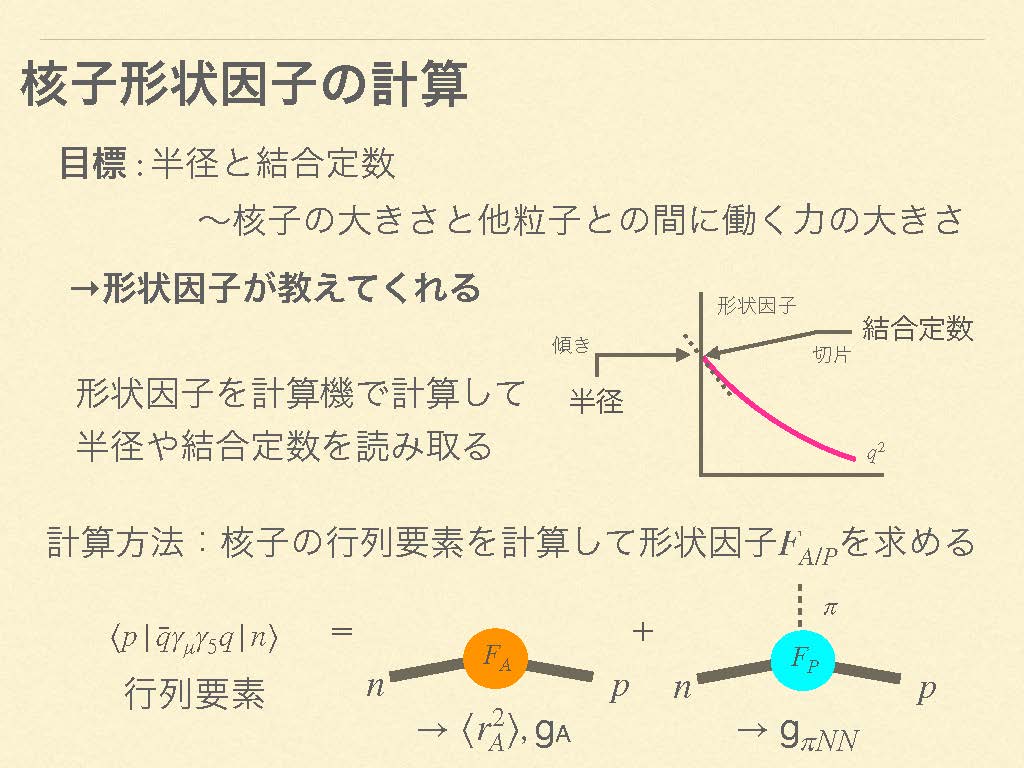
核子は単なる粒子ではなく、素粒子のクォークやグルーオンが絶えずできたり消えたりする非常に複雑な内部構造をとっています。この内部構造が散乱のしかたに影響を与えます。ここで重要な関数が「形状因子」です。
形状因子は「核子の形や大きさが、衝突する確率にどのように影響するか」を記述する関数で、散乱断面積を計算する際に、補正項として現れ、核子の電荷密度分布（核子を構成するクォークの空間的広がり）などを反映しています。形状因子の値を実験により測定することで、核子の内部構造を間接的に知ることができます。つまり、散乱断面積は形状因子によって決まるのです。形状因子が大きい領域では散乱断面積は大きく、小さい領域では小さくなります。
また、ニュートリノが核子に衝突すると、ニュートリノの運動量の一部が核子に移行します。これを「運動量移行（q2）」といいます。実験結果からは、運動量移行（q2）が大きくなると形状因子は減衰していくと考えられており、特にいくつかの形状因子は双極子型の曲線を描くことが予想されています。
形状因子は運動量移行（q2）に対する関数として表されます。核子の内部構造に関する情報を得るための指標として、この関数のグラフの「切片」と「傾き」が使われています（図2）。まず、切片は核子がもつ電荷や磁気の大きさに対応しています。また、傾きは核子の半径に対応しています。傾きが急であれば核子の分布が大きく、緩やかであれば核子の分布が小さく密集しています。
図2：核子の内部構造に関する情報を得るための指標として、形状因子のグラフの「切片」と「傾き」が使われている。
ニュートリノが核子と衝突する際に起こる反応の1つに「準弾性散乱」があります。準弾性散乱とは、ニュートリノが核子に衝突した際に、核子を分解することなく、中のクォークの種類だけが入れ替わる現象のことです。たとえば、ミューニュートリノが中性子に衝突すると、中性子は陽子に変わり、同時にニュートリノはミューオンという素粒子に姿を変えて外に飛び出します。中性子は陽子に変化しますが、分解されるわけではないので、「準弾性」と呼ばれています。
このとき、核子は壊れずに残りますが、運動量やエネルギーは変化します。ここで、準弾性散乱を理解するために重要なのが形状因子です。準弾性散乱の測定結果を形状因子に入力することで、電荷分布など内部構造の細かい情報を理論的に、数値として確認することができるのです。
「しかし、ここで大きな課題があります。準弾性の散乱断面積（衝突の確率）を計算する式には、『軸性形状因子（FA）』と呼ばれる形状因子が含まれています。そして、この軸性形状因子が最も大きな不定性を抱えており、散乱過程の記述の高精度化に向けた障壁になっているのです」（辻さん）。
クォークは電荷や磁気だけでなく、スピンによる性質ももっています。ニュートリノは電磁相互作用ではなく、弱い相互作用（弱い力）によって核子と関わります。そのため、核子内部のスピンに関する情報が弱い相互作用に強く影響します。この核子内部のスピンの分布を表すのが、軸性形状因子（FA）です（図3）。
「軸性形状因子（FA）が最も大きな不定性を抱えている理由は、実験により高精度な測定データを得ることができないからです。現在は、安全性の面から実験を実施することができず、今なお50年以上前の測定データが使われているのが現状です。そこで、スーパーコンピュータ『富岳』と我々数値計算グループの出番というわけです」（辻さん）。
図3：最も大きな不定性をもつ軸性形状因子（FA）を数値計算により高精度で計算することで、CP対称性の破れの謎の解明や新たな物理の発見につながる。
「核力」を扱う「格子QCD」が抱える誤差
クォークとグルーオンの間には「強い相互作用（強い力）」が働いています。この強い相互作用を扱うのが「量子色力学（QCD）」と呼ばれる理論です。しかし、強い相互作用は非常に複雑なため、スーパーコンピュータをもってしても数値計算が困難です。そこで現在「格子QCD」と呼ばれる数値計算手法が用いられています。
格子QCDは、連続した空間と時間を小さなマス目（格子）状に区切り、その中にクォークとグルーオンを配置し、確率的にどのように動くかを、膨大なサンプルを使ってスーパーコンピュータで数値計算します。これにより、核子の質量や形状因子、核子間の相互作用などを実験に依存せず、「第一原理」に基づき理論的に導き出すことができます。
一方で、格子QCDには「統計誤差」と「系統誤差」という2種類の誤差があります。まず、統計誤差は、ランダムなサンプリングによって生じる誤差です。格子QCDでは、クォークとグルーオンの配置を確率的に生成して平均を取るため、サンプル数が有限だと揺らぎが生じてしまいます。統計誤差を減らすためにはサンプル数を増やすしかありません。
また、系統誤差は、数値計算の方法そのものによって生じる誤差です。たとえば、系統誤差としては、「離散化誤差」が挙げられます。離散化誤差は、空間や時間を連続ではなく、離散的な「格子」という点の集まりで近似するために生じる誤差です。格子間隔が粗いと、本来の滑らかな変化を正しく表すことができません。格子を細かくしていき、「連続極限」を取ることで、誤差を小さくすることができます。
系統誤差には、「有限体積効果」と呼ばれるものもあります。これは、計算に使う仮想空間の大きさ（体積）が有限であるために起こる誤差です。実際の物理現象は、無限に広がる空間で起こりますが、計算では有限の箱の中でしか扱えないため、粒子が自分の像と干渉したり、長距離の相互作用を計算に含められなかったりすることで誤差が生じるのです。これを抑えるには、計算に使う体積をできるだけ大きくする必要があります。
このように、格子QCDの結果には統計誤差と系統誤差があるため、両方を考慮して、結果の信頼性を評価する必要があるのです。
高精度化のポイントは「巨大体積」と「物理点」
「そこで、我々のグループが取り組んでいるのが、巨大体積下における物理点での格子QCD計算です。ポイントは、巨大体積であることと、物理点のみで計算することです」（辻さん）。
まず、巨大体積とは、計算に使う空間の体積を十分大きくすることです。空間の体積が小さいと核子の周りの“場”が制限されるため、電荷分布や磁気分布が過小評価されたり、有限体積効果による誤差が大きくなったりします。そのため、高精度な数値計算ができません。それに対し、巨大体積を使うことで、実際の物理現象により近い条件を再現できます。
次に、物理点とは、数値計算に用いるパラメータが現実の物理値に近い状態を指します。物理点で計算することで、不定性を減らすことができるため、数値計算の結果と現実の核子の内部構造が高精度で一致するようになります。これにより、数値計算結果を実際の実験結果と直接比較できるようになります。
このように、格子QCDを使って核子の形状因子を数値計算する際、巨大体積と物理点での数値計算が重要なのは、現実の核子のもつ内部構造をコンピュータで再現した核子に正確に反映させるためなのです。
「つまり、巨大体積により系統誤差をできる限り低減し、物理点により現実に近い核子を再現することで、形状因子をより正確に高精度で数値計算しようというのが、我々の戦略です」（辻さん）。
10年間の取り組みで他を圧倒する成果を達成
そして、辻さんのグループは、不定性が最も大きな軸性形状因子（FA）にターゲットを絞り、スーパーコンピュータ「富岳」を使い、巨大体積下による物理点での格子QCD計算を実施しました。
実際に数値計算を行ったのが「軸性形状因子」です。また、軸性形状因子をデータ解析することで、「軸性電荷」と「軸性半径」を求めました。これらは核子の中でのクォークのスピンの分布の様子を調べるための指標です。
まず、軸性形状因子は、核子の内部におけるスピンの分布の情報を表す関数です。これは運動量移行（q2）、すなわち核子がどれくらい強く叩かれたかを示す量に依存して変化します。そして、その軸性形状因子を、運動量移行（q2）がゼロのときに評価した値が、軸性電荷です。軸性電荷は、核子がもつスピンにクォークがどのくらい寄与しているかを示す定数で、核子の基礎的な特性の1つと考えられています。さらに、軸性形状因子がどのくらいの広がりを持つかを表す量が軸性半径です。これは、軸性形状因子の運動量依存性を調べ、その変化のしかた（関数の傾き）によって定義されます。軸性半径は、スピンの分布が核子内部でどのくらい広がっているかを示す指標です。
軸性形状因子を調べる際、特に重要なのが、運動量が小さい領域（低運動量領域）における情報です。低運動量領域では、軸性形状因子の値は、軸性電荷と呼ばれる基本的な定数に直接つながるため、弱い相互作用を説明する上でとても重要です。また、低運動量領域からは、軸性半径を示す指標も得られます。低運動量領域は実験が非常にむずかしい領域であるため、より高精度で数値計算ができれば、弱い相互作用の性質を理解する上で大きなメリットがあるのです。
「このように、物理点での低運動量領域を調べることで、T2K実験に最も貢献できる形で核子の内部構造を理解できることから、我々は低運動量領域に限定し、巨大体積下における物理点での格子QCDを実行したのです」（辻さん）。
実際の数値計算の結果は次の通りです。
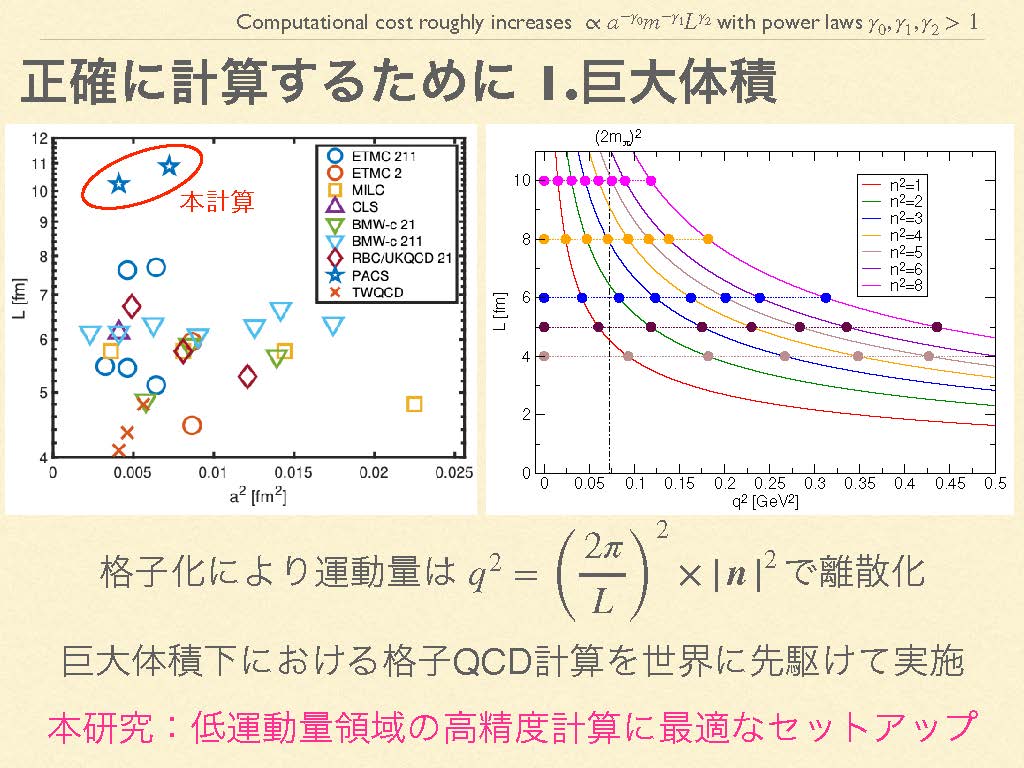
まず、図4左のグラフは横軸に時空間の区切り幅、縦軸に空間の一辺の長さを取っています。区切り幅が狭いほど、空間が大きいほど数値計算は大変になりますが、より現実に近い数値を得ることができます。また、図4右のグラフは、空間が大きいほど（上に行くほど）運動量移行（q2）を細かく離散化して計算できることを示しており、これも計算精度の向上につながります。
「我々のグループの数値計算は他のグループの中で群を抜いて、巨大体積かつ高精細であることがわかります。我々が他に先駆けてこのような成果を達成できたのは、我々の先輩方がスーパーコンピュータ『京』の時代から約10年もの歳月をかけてコツコツと取り組んできたからにほかなりません」（辻さん）。
図4：辻さんたちが行った計算のセットアップ。区切り幅が狭いほど、空間が大きいほどより現実に近い数値を得ることができる。辻さんのグループの数値計算は他のグループの中で群を抜いていることがわかる。
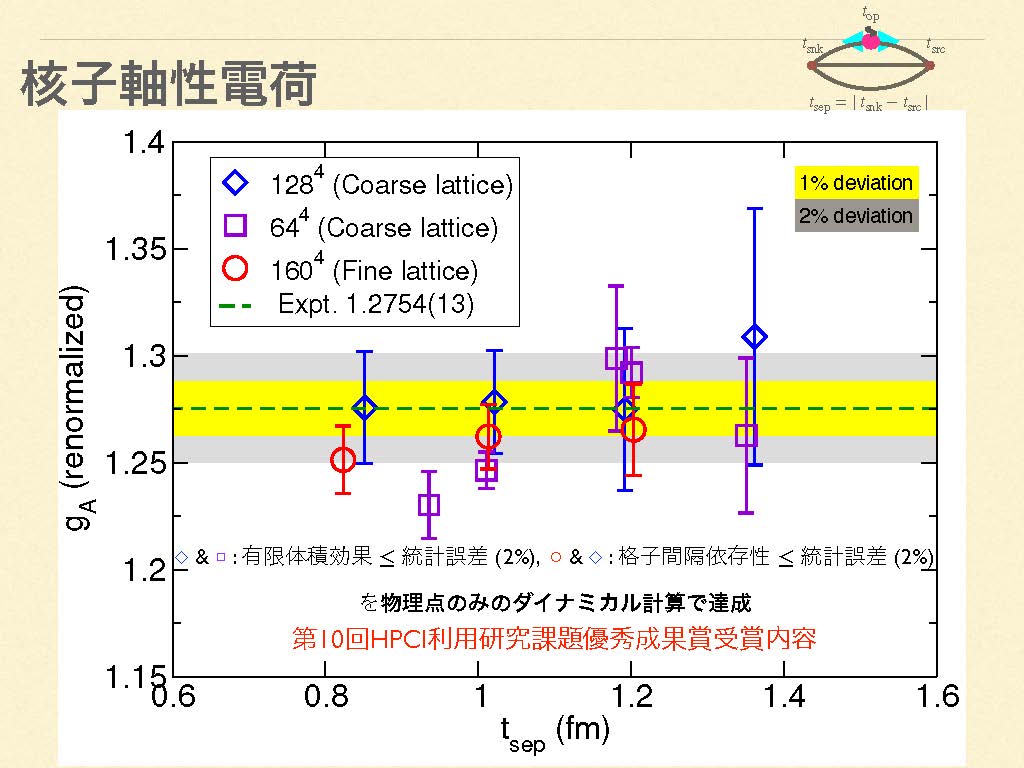
「また、物理点のみで数値計算を行うことにより、軸性電荷に対しては有限体積効果と格子間隔依存性が非常に小さく、ともに2％の統計誤差の範囲内で無視できることがわかりました（図5）」（辻さん）。
この成果が高く評価され、2023年10月、辻さんのグループの「格子QCDを用いた素粒子原子核物理の精密計算」（課題代表者：東北大学 佐々木勝一准教授）は、「第10回HPCI利用研究課題優秀成果賞」を受賞しました。
「核子の研究の最終目標は、CP対称性の破れの謎の解明への貢献と新たな物理の発見です。そのためには、理論と実験と数値計算、それぞれの研究者が協力し合いながら進めていくことが不可欠です。今後も、数値計算の立場から、最終目標に向けてさらなる高精度化に取り組んでいきます」（辻さん）。
図5：軸性電荷について、物理点のみで数値計算を行うことで、有限体積効果と格子間隔依存性が非常に小さく、ともに2％の統計誤差の範囲内で無視できることが判明した。
