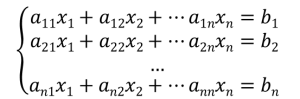宇宙現象などのシミュレーションには、膨大な量の計算が必要です。さらに近年では、問題のサイズがどんどん大規模になっています。そのため、扱っている問題を計算するにあたり最適なアルゴリズムや高速化の手法をみつけることが重要です。中でも、計算時間の大半を費やしている連立一次方程式の解を高速で効率よく求めることができれば、宇宙や原子核など様々な分野の研究の進展に役立ちます。
筑波大学計算科学研究センター研究員の今倉 暁(いまくら・あきら)さんは「連立一次方程式と聞くと難しく思うかもしれませんが、小学校で習った「鶴亀算」と同じなのですよ」といいます。今倉さんは、超新星爆発シミュレーションにおける連立一次方程式を解くための手法を研究しています。
問)鶴と亀が合わせて8匹います。足の合計は26本でした。鶴と亀はそれぞれ何匹いますか?
解き方)鶴と亀合わせて8匹、足の数が全26本の場合、8匹すべてが亀だとすると足が6本多い。鶴は亀より足が2本少ないので、1匹亀を鶴に変えると2本足が減る。足を6本減らすには、亀を3匹鶴に変えればよい。すると鶴が3匹、亀が5匹で、足が26本になる。
答え)鶴が3匹、亀が5匹
連立一次方程式は、行列とベクトルで記述される
「鶴と亀が合わせて8匹います。足の合計が26本でした。 鶴と亀はそれぞれ何匹いますか?」この鶴亀算は、鶴の数をx亀の数をyと置くと、変数x、yについての連立一次方程式
で表されます。鶴亀算は一般に「全て鶴だとすると・・・」もしくは「全て亀だとすると・・・」として解きますが、これは連立一次方程式の各式を変形し、変数を消去することに対応しています(図1)。
鶴亀算では変数は鶴の数xと亀の数yの2つでしたが、超新星爆発などの大規模なシミュレーションでは、変数の数が1000万や1億もあるような非常に大規模な連立一次方程式が現れます。一般に、変数がx1、x2…、xnのようにn個ある連立一次方程式は、
のように表されます。この式は図2のように係数a11~annをn次行列、変数x、定数bをn次元ベクトルとして、Ax=bのように表現することができます。連立一次方程式を解くということは、与えられた行列Aとベクトルbに対して、Ax=bを満たすベクトルxを求めることなのです(図2)。このように、連立一次方程式を一般化して解き方を考えることで、変数の数や係数の値によらずどのような連立一次方程式に対しても、同様の方法で解くことができるようになります。
連立一次方程式の解を求める方法には、大きく分けると直接法と反復法があります。図1のように式の変形により変数を消去していく方法は代表的な直接法で、「ガウスの消去法」と呼ばれます。一方、反復法は、適当に選んだ初期値から計算を繰り返して反復的に近似解を求め、その解が十分に真の解に近づいたところで計算を打ち切り、解とする方法です。
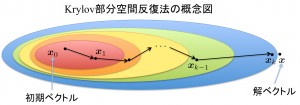
直接法は、どんな問題でも原理的には厳密な解を求めることができるのですが、問題の規模が大きくなると、時間がかかりすぎてしまい、なかなか解にたどりつくことができません。そこで、大規模な計算では反復法を使います。中でも、よく使われる反復法は「クリロフ部分空間法」です。クリロフ部分空間とはn次行列とn次元ベクトルの積でつくられるベクトル空間をいいます。反復によってクリロフ部分空間をつくり、その中で連立一次方程式の近似解を求める方法です。初期値から反復により空間を広げながら近似解を更新します(図3)。
前処理で収束性を改善
クリロフ部分空間法は、直接法と比べて少ない計算量で解けるのですが、計算の仕方によっては収束性が悪く、解ける問題が限られるのが難点でした。収束するとは、計算した値が解に向かって限りなく近づくことです。反復するうちに値が収束するとはいえ、なかなか収束しなければ計算量は増え、精度も悪くなってしまいます。
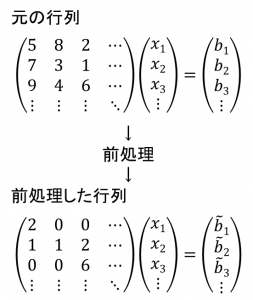
クリロフ部分空間法には、係数行列Aが単位行列※1に近い場合、少ない反復回数で収束するという特徴があります。そこで、単位行列に近くなるように係数行列を変形し、収束性を改善させることを考えます(図4)。これを「前処理」と呼びます。つまり、収束性は係数行列Aの固有値の分布に依存し、固有値が密集していれば高速に収束するので、元の係数行列によく似た前処理行列を使って固有値の分布を改善します。そして、前処理行列によって元の方程式を変換し、反復法で解を求めます。変形した連立一次方程式の係数行列の固有値が密集していれば、クリロフ部分空間法は高速に収束することが期待されます。
前処理にも不完全LU分解前処理、近似逆行列前処理、定常反復法前処理など様々な種類があり、それぞれにいろいろな手法があります。解きたい問題に適した前処理を行えば劇的に収束性がよくなり、反復回数や時間を短縮できます。
重みパラメータの最適化法を考案
今倉さんは、超新星爆発のシミュレーションに向け、反復法の一種「ヤコビ法」を使った重み付きヤコビ反復型前処理に着目しました。ヤコビ法は古くから使われる反復法の一種ですが、これをクリロフ部分空間法の前処理として使うというアイデアです。
「ヤコビ反復型前処理は、シミュレーションの大規模計算に必要な並列化に向くのですが、収束性がよくないのです。そこで、重みパラメータ(変数)を設定して計算し、収束を加速させようとしました。そうすれば収束性もよくなり、計算も楽になると考えたのです」。
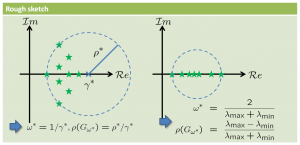
図5 反復行列の固有値の分布。円の中心の逆数がパラメータの最適値になる反復行列の固有値の分布を近似的に計算します。その固有値分布がわかれば最適な重みパラメータを自動的に計算できるというわけです。計算された重みパラメータを適用して、ヤコビ反復型前処理を行います。
けれども、問題によって最適な重みパラメータは変わってしまいます。重みパラメータはユーザーが自身で決めるものですが、最適でないものを使えば収束性はよくなるどころか、悪くなってしまう可能性もあります。そこで、今倉さんは、重みパラメータを問題ごとに自動的に最適化する方法を考案しました。収束性は、ヤコビ前処理の反復でできる反復行列の性質に依存します。これを利用して重みパラメータと収束性の関係式を求めました。またその式から、反復行列の固有値※2の分布がわかれば固有値を囲む円が求まり、円の中心の値の逆数がパラメータの最適値になることがわかりました(図5)。
超新星爆発の計算が10倍速く
新たに考案した前処理の技法がクリロフ部分空間法を解くのに有効であるかどうかは、数値実験から確認しました。少ない計算コストで重みパラメータを最適化でき、多くの問題に対して前処理の性能が向上したことがわかりました。
「この前処理法により、超新星爆発の計算が従来の方法より10倍は速くなりました。今までなかなか解にたどりつけなかった問題も解けるようになりました」と今倉さん。これからはこの手法を実際の超新星爆発シミュレーションのための計算に応用していきます。実際に計算を行う共同研究者たちも、この結果に喜んでいるようです。
今倉さんは、2011年4月に名古屋大学から筑波大学計算科学研究センターに移ってきました。「今まで理論中心の基礎研究をしてきたので、シミュレーションなどの応用に向けた計算の研究はこれが初めてです。そのため、この研究は印象深いものとなりました」と感慨深げに話します。「筑波大学に来て、このような機会を得ることができました。研究の成果が新しい物理の発見などに貢献できるといいなと思います」。
こうした計算手法に対する研究が宇宙分野のみならず素粒子や原子核などの研究の発展につながるのです。今倉さんのこれからの活躍が期待されます。
用語解説
※1 単位行列:正方行列のうち、右下がりの対角線上にある成分が すべて1で、残りの成分がすべて0の行列。
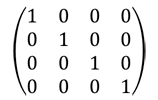
※2 固有値:線形空間で、あるベクトルを線形変換した結果が、そのベクトルの定数倍に等しくなる時のその定数(1個とは限らない)。
行列![]() において、
において、![]() をみたす実数
をみたす実数![]() が存在するとき、
が存在するとき、![]() を行列
を行列![]() の固有値という。
の固有値という。
![]() の固有値は、
の固有値は、![]() の解で与えられる。
の解で与えられる。