1 線形方程式の解法の選択
2 参考文献および参考書の記述
線形方程式, 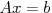 >>> 実非対称/複素非エルミート,
>>> 実非対称/複素非エルミート, 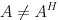 >>> 安定性重視 >>> リスタート版: >>> FOM(m) 法
>>> 安定性重視 >>> リスタート版: >>> FOM(m) 法
概要 †
- FOM(m)法は1981年にSaadによって提案された非エルミート線形方程式向けのKrylov部分空間法である.
- リスタート
- アルゴリズムの反復を所定のリスタート周期
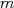 で停止し, 得られた近似解を初期近似解として再びアルゴリズムを適用する.
で停止し, 得られた近似解を初期近似解として再びアルゴリズムを適用する.
- リスタートを適用することで, Arnoldi原理の長い漸化式に由来するFOM法の問題点を解決出来る.
一方で, 収束性は悪化する.
導出 †
準備中
アルゴリズム †
FOM(m)法 †
- Set an initial guess
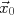
- Compute
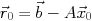
- Set
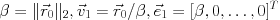
- For
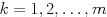
-

- For
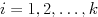
-
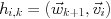
-
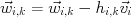
- End For
-
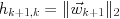
-
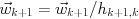
- For

-
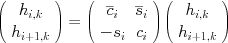
- End For
- If
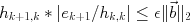 or
or  then
then
-
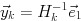
-
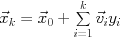
- exit
- End If
-
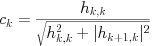
-
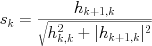
-
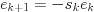
-
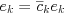
-
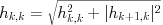
-
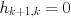
- End For
- Set
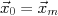 and go to 2
and go to 2
前処理付きFOM法 †
- Set an initial guess
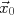
- Compute
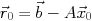
- Set
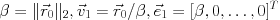
- For
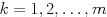
-
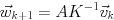
- For
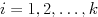
-
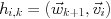
-
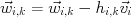
- End For
-
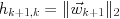
-
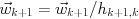
- For

-
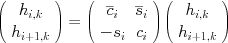
- End For
- If
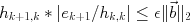 or
or  then
then
-
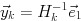
-
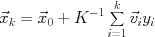
- exit
- End If
-
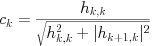
-
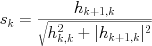
-
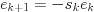
-
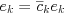
-
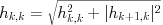
-
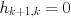
- End For
- Set
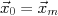 and go to 2
and go to 2
サンプルプログラム †
準備中
適用事例 †
準備中
参考文献および参考書 †
原著論文 †
[13] Yousef Saad, Krylov subspace methods for solving large unsymmetric linear systems, Mathematics of Computation 1981; 37(155):105–126.
教科書 †
[14] Yousef Saad, Iterative Methods for Sparse Linear Systems, 2nd ed., SIAM: Philadelphia, PA,
2003.
P159–161
![[JICFuS Wiki] [JICFuS Wiki]](image/pukiwiki.png)