“For those of us interested in the deepest and the most fundamental rules of the universe, there are two things we need to understand. One is the smallest building blocks of matter — quarks — and the other is the force that holds them together — the strong force.” — Dr. Yu Zhang of RIKEN RCCS.
“For those of us interested in the deepest and the most fundamental rules of the universe, there are two things we need to understand. One is the smallest building blocks of matter — quarks — and the other is the force that holds them together — the strong force.” — Dr. Yu Zhang of RIKEN RCCS.
The strong force
According to the Standard Model, there are 17 elementary particles (Fig.1). Twelve of them are quarks and leptons, which make up matter. Four of the others — the gluon, photon, and W and Z bosons — are the carriers of forces. The last, the Higgs boson, is a bit different and is thought to be the origin of mass.
“There are four fundamental forces in nature — gravity, the electromagnetic force, the strong force, and the weak force. Gravity has not been included in the Standard Model yet. The electromagnetic force is mediated by photons, the strong force by gluons, and the weak force by W and Z bosons. The strongest force in the universe is the strong force. And this is what I’m interested in,” Dr. Zhang said.
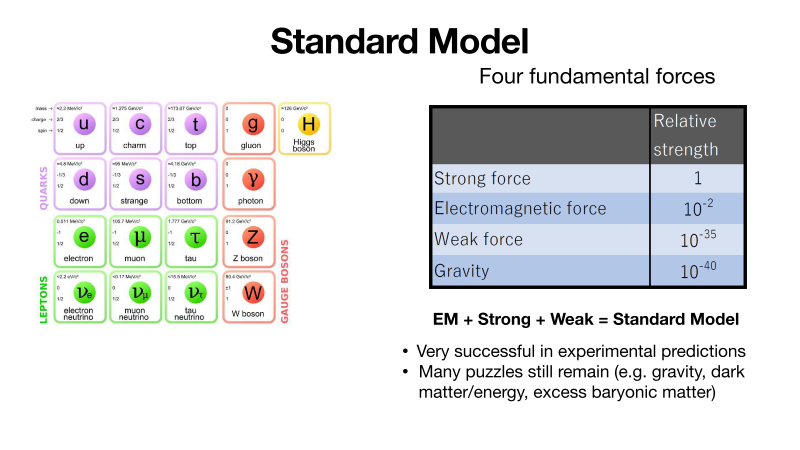
Fig. 1 Standard Model
The Standard Model explains the smallest particles of matter and the forces that combine them to make up all matter.
The strong force is mediated by gluons, which hold two or three quarks together to build up a variety of hadrons, such as protons and neutrons. Gluons also keep the atomic nuclei intact.
QCD is the theory that describes the strong interaction between quarks and gluons. There are six “flavors” of quarks — up, down, strange, charm, bottom, and top.
The field is called chromodynamics because quarks must have an additional quantum number, called the color. (This is just a metaphor, not the color we see in our daily life.) For the quarks, they are red, green, and blue. Anti-quarks are designated with complementary colors (cyan, magenta, and yellow).
Quarks should be combined to form a colorless hadron. For example, a proton consists of a red up quark, a blue up quark, and a green down quark. A π-meson consists of a green up quark and a magenta down anti-quark. In both cases, the sum of the colors is white. This rule means that quarks in a hadron cannot be pulled apart. In other words, quarks are confined in a hadron. The majority of a hadron’s mass actually comes from the energy of the gluons that bind quarks together.
“In this low-temperature world, the quarks and gluons are confined in hadrons, but in the extremely high T or density, they are expected to be free. We want to know how some microscopic amount of strong interacting matter responds to changes in the external control parameters, for example the temperature or the baryon chemical potential. So we look at the thermodynamics of QCD, and we need the lattice to study it.”
Lattice QCD
When you want to study the strong interacting matter that is created in heavy ion experiments in theoretical calculations it’s difficult to do it on a piece of paper — you need big computers for that. What do you put on this computer? You try to put the theory of strong interactions which is QCD. The way to do this we learned in the early 1960s from Richard Feynman that the thermodynamics or the field theory of strong interactions can be formulated as a path integral, which is described by an infinite dimensional over the gluon fields and the quark fields.
Lattice QCD simulation is basically to brute force evaluate those path integrals by working on a discrete space-time – with lattice spacing \(a\) and quark field on each lattice point and gluon fields on each link (Fig.2). Then the path integral becomes finite-dimensional and can be evaluated by the Monte Carlo method. Its dimension is very large and typically calculated on supercomputers.
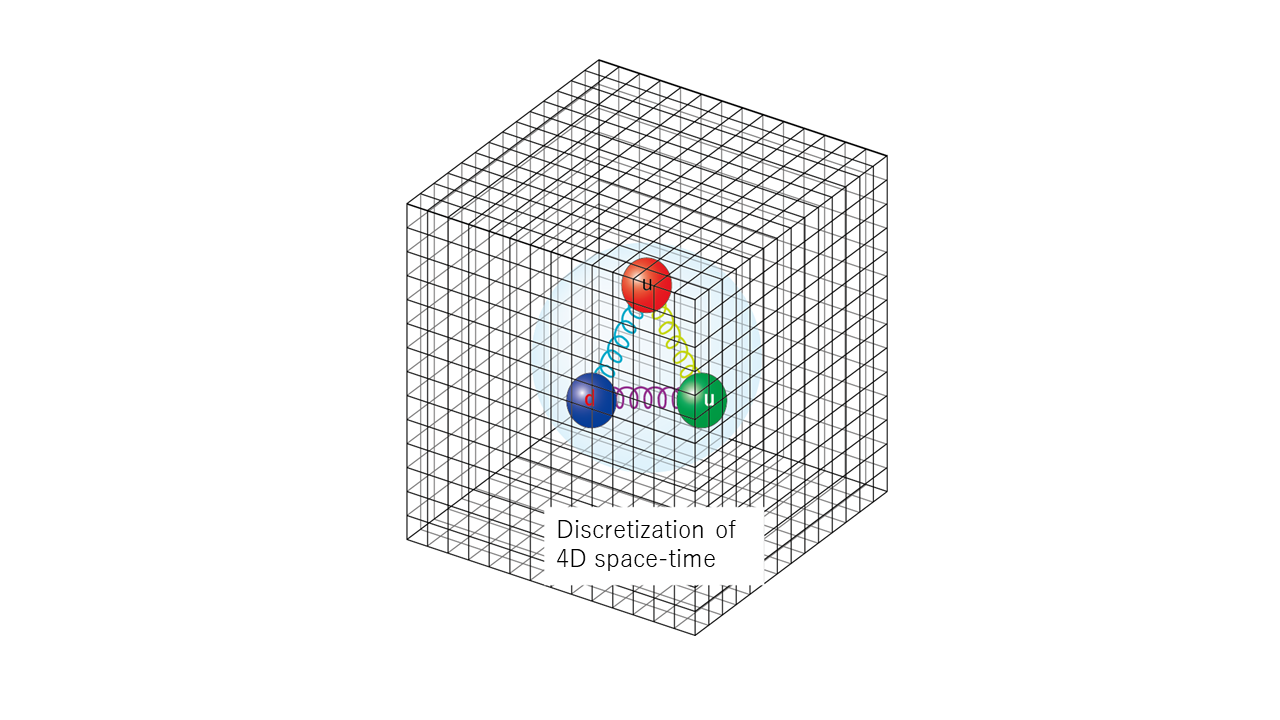
Fig. 2 Image of the lattice QCD
Quarks are drawn as balls, gluons as strings.(Courtesy Dr. Ken-Ichi Ishikawa)
QCD phase transition
QCD is expected to undergo a phase transition at a certain finite temperature and density, as shown in Fig. 3. In this phase transition the quarks, as well as gluons, in hadrons should be released to make a quark-gluon plasma, a new phase of matter.
These phase transitions are interesting because they are related to the early universe and the structure of neutron stars. Additionally, they are thought to reveal an important property of QCD, called “chiral symmetry breaking.” At temperatures lower than the critical temperature, the quarks are confined in hadrons, and the chiral symmetry is broken. At temperatures higher than the critical temperature, the chiral symmetry is restored.
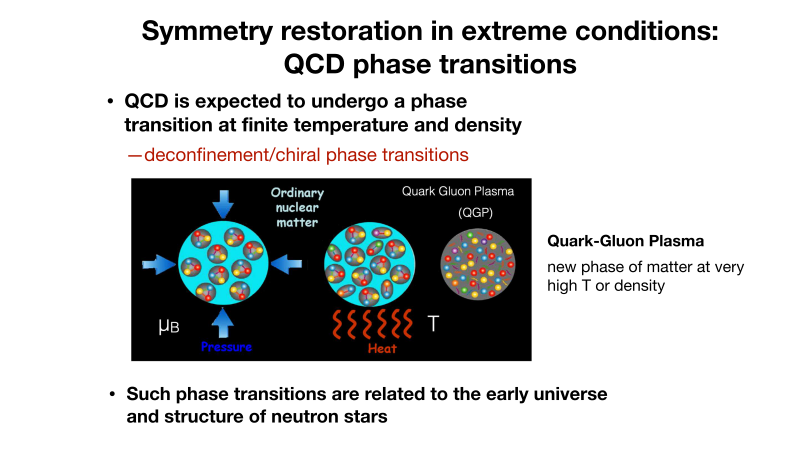
Fig. 3 Phase transition in QCD
Source of schematic diagram:
https://www.olcf.ornl.gov/wp-content/uploads/2013/02/Swagato_LQCD.pdf
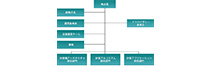
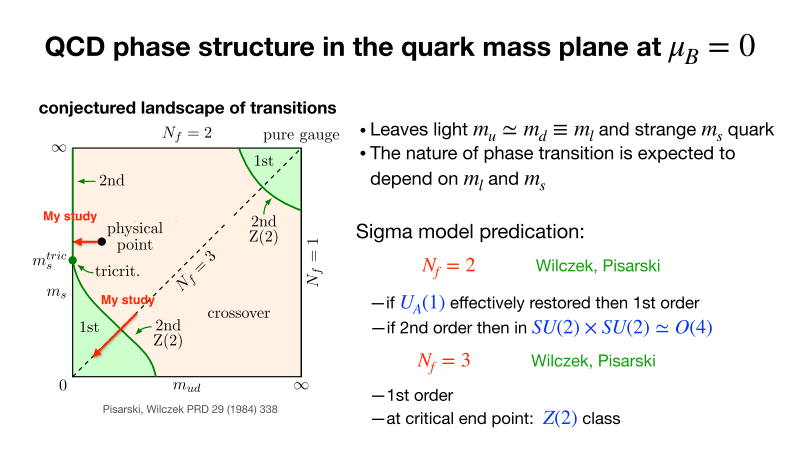
The character of the phase transition is thought to depend on the mass of quarks and the number of degenerated quark flavors, \(N_f\). But the detailed phase structure has not been made clear. “What I’m currently working on is to see whether there is a first order phase transition in the 3 flavor chiral regime. And if so, what is the critical mass which separates the first order and crossover transition?” Her research includes two kinds of \(N_f\) s (Fig.4).
For her Ph.D. work, Dr Zhang investigated the chiral phase structure of (2+1)-flavor ( \(N_f\) =2+1) QCD from the lattice QCD simulations with values of quark masses decreasing towards the chiral limit along the red horizontal arrows shown in Fig.4. \(N_f\)=2+1 represents that two of the three quarks are degenerated but one is not. The order of the QCD phase transition depends on whether the UA(1) symmetry is effectively restored at the critical temperature. “This is kind of hard because when the quark mass becomes smaller and smaller, you need more computation time.”
“How the axial anomaly manifests itself affects the nature of the chiral phase transition, and is a fundamental question in QCD,” Dr. Zhang said, explaining the results shown in Fig.5. “We performed a first continuum and chiral extrapolation of UA(1) measures in (2+1)-flavor lattice QCD at T=205 MeV. We found that the axial anomaly remains manifested at T=205 MeV and this strongly suggests the chiral phase transition is second order.”
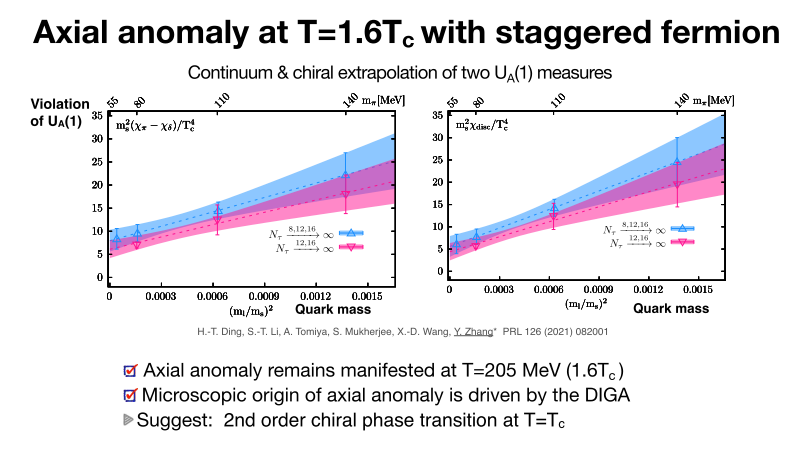
Fig. 5
The continuum result of \( \chi_{\pi} – \chi_{\delta} \) and \(\chi\)disc at T=205 MeV with (2+1)-flavor of staggered quarks.
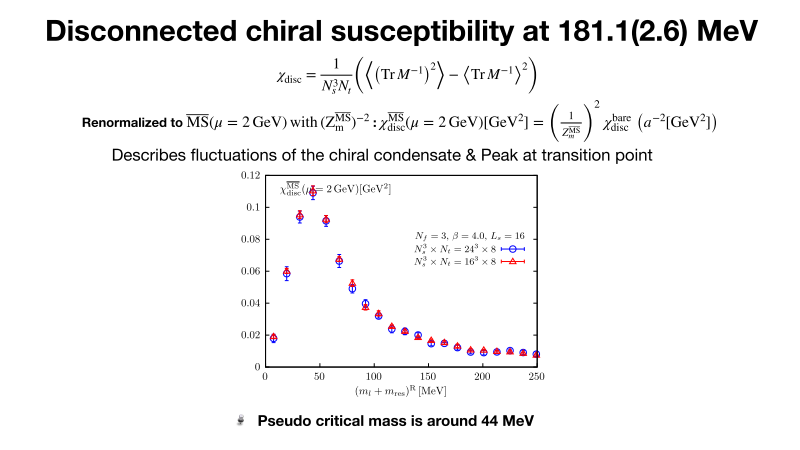
In her more recent study, she and her collaborators are investigating the QCD phase structure with three degenerate quark flavors using a chiral fermion which respects the chiral symmetry. Dr. Zhang is looking at the volume and quark mass dependence of disconnected chiral susceptibility at T=181 MeV as shown in Fig.6. The peak location of disconnected chiral susceptibility indicates the transition point and there is no volume dependence. These results tell us that it’s a crossover transition at T=181 MeV and the pseudo critical mass is around 44 MeV.”
Dr. Zhang needs a lot of computational resources in her research. “For example, in this current three-flavor study, we are using the chiral fermion, which is good because it possesses chiral symmetry and that is important for our study. But it requires large computational cost, because we are interested in this small quark mass regime. Since the number of iterations rapidly increases as the quark decreases, so does the cost of simulations.”
Coming to Japan
“I came to Japan and joined RIKEN after I finished my Ph.D. program, which was about the axial UA(1) symmetry at high temperature in \(N_f\) =2+1 lattice QCD with staggered (non-chiral) fermions. I proposed a novel method and found that at T=205 MeV the axial UA(1) symmetry remains broken.”
“This is a longstanding problem — Japan’s lattice QCD group JLQCD often uses chiral fermions to study this problem and they have come to different conclusions.”
“The chiral fermion is important for our study and I wanted to confirm the staggered fermion result using chiral fermion and the proposed novel method, so I came to Japan to further explore this problem.”
Dr. Zhang added: “Also, here at RIKEN, I have access to the Fugaku supercomputer, as well as the Wisteria at the University of Tokyo.”
Lattice QCD is computationally intensive, to put it mildly. The number of calculations required to create such a simulation is enormous and can rise into the billions per second, for which supercomputers providing teraflops of processing power are required. That is why the RIKEN R-CCS Fugaku supercomputer is a crucial component of this work.