![[JICFuS Wiki] [JICFuS Wiki]](image/pukiwiki.png)
![[JICFuS Wiki] [JICFuS Wiki]](image/pukiwiki.png)
1 線形方程式の解法の選択
2 参考文献および参考書の記述
線形方程式, 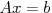 >>> 実非対称/複素非エルミート,
>>> 実非対称/複素非エルミート, 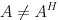 >>> その他 >>> マルチグリッド法: >>> 幾何的マルチグリッド法
>>> その他 >>> マルチグリッド法: >>> 幾何的マルチグリッド法
偏微分方程式を離散化して得られる方程式
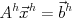 ・・・(1)
・・・(1)に対してJacobi法やGauss-Seidel法などの定常反復法を適用すると, 誤差の持つ空間的高周波成分が速く減衰すること(平滑化作用)が知られている. このため空間的低周波成分で構成される粗い格子に対応する低次元の方程式
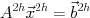 ・・・(2)
・・・(2)を用いて, 方程式(1)の近似解の精度を効率的に改善できることが期待される. この方法を2段グリッド法と呼ぶ.
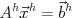 に対し定常反復法を数反復適用し近似解
に対し定常反復法を数反復適用し近似解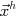 を得る.
を得る.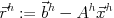 の粗い格子への制限(restriction)
の粗い格子への制限(restriction) を計算する.
を計算する.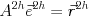 を解く.
を解く.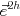 の補完(interpolation)
の補完(interpolation)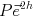 を用い, 細かい格子上の近似解を
を用い, 細かい格子上の近似解を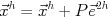 と修正する.
と修正する.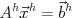 に対し
に対し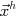 を初期近似解として, 定常反復法を数反復適用し近似解
を初期近似解として, 定常反復法を数反復適用し近似解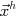 を得る.
を得る.[14] Yousef Saad, Iterative Methods for Sparse Linear Systems, 2nd ed., SIAM: Philadelphia, PA,
2003.
P407–449
[23] Masaaki Sugihara and Kazuo Murota, Theoretical Numerical Linear Algebra, Iwanami Press: Tokyo, 2009, (in Japanese).
P106–136