![[JICFuS Wiki] [JICFuS Wiki]](image/pukiwiki.png)
![[JICFuS Wiki] [JICFuS Wiki]](image/pukiwiki.png)
1 線形方程式の解法の選択
2 参考文献および参考書の記述
線形方程式, 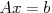 >>> 実非対称/複素非エルミート,
>>> 実非対称/複素非エルミート, 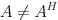 >>> 安定性重視 >>> GCR 法
>>> 安定性重視 >>> GCR 法
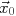 , 対応する初期残差を
, 対応する初期残差を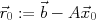 と置く.
この時, GCR法の
と置く.
この時, GCR法の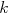 反復目の近似解
反復目の近似解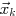 は,
は,
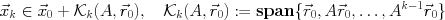
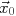 とクリロフ部分空間
とクリロフ部分空間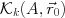 で張るアフィン空間に含まれ, 残差ベクトル
で張るアフィン空間に含まれ, 残差ベクトル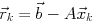 が
が
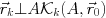
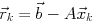 は, 最小残差条件
は, 最小残差条件
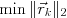
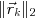 の単調減少性が保証される.
の単調減少性が保証される.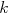 の増加に伴って, 反復当たりの演算量および記憶容量が増大する.
このため, 実用上はリスタート版のGCR(m) 法やトランケート版のORTHOMIN(m) 法が用いられる.
の増加に伴って, 反復当たりの演算量および記憶容量が増大する.
このため, 実用上はリスタート版のGCR(m) 法やトランケート版のORTHOMIN(m) 法が用いられる.準備中
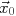
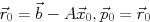
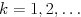
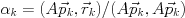
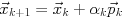
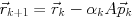
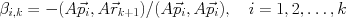
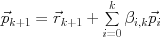
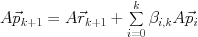
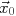
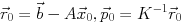
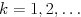
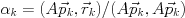
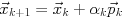
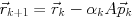
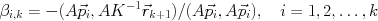
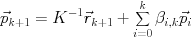
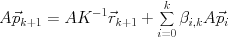
準備中
準備中
[5] Stanley C. Eisenstat, Howard C. Elman and Martin H. Schultz, Variational iterative methods for nonsymmetric systems of linear equations, SIAM Journal on Numerical Analysis 1983; 20(2):345–357.
[14] Yousef Saad, Iterative Methods for Sparse Linear Systems, 2nd ed., SIAM: Philadelphia, PA,
2003.
P194–196
[23] Masaaki Sugihara and Kazuo Murota, Theoretical Numerical Linear Algebra, Iwanami Press:
Tokyo, 2009, (in Japanese).
P164–173
[29] 藤野 清次, 張 紹良, 反復法の数理 (応用数値計算ライブラリ) 朝倉書店, 1996.
P63–70