![[JICFuS Wiki] [JICFuS Wiki]](image/pukiwiki.png)
![[JICFuS Wiki] [JICFuS Wiki]](image/pukiwiki.png)
1 線形方程式の解法の選択
2 参考文献および参考書の記述
線形方程式, 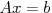 >>> 実対称/複素エルミート,
>>> 実対称/複素エルミート,  >>> 正定値 >>> CG 法
>>> 正定値 >>> CG 法
 対応する初期残差を
対応する初期残差を と置く.
また, 線形方程式
と置く.
また, 線形方程式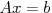 の真の解を
の真の解を と置く.
この時, CG法の
と置く.
この時, CG法の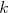 反復目の近似解
反復目の近似解 は,
は,
 ・・・(1)
・・・(1) とクリロフ部分空間
とクリロフ部分空間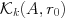 で張るアフィン空間に含まれ, アフィン空間上で2次関数
で張るアフィン空間に含まれ, アフィン空間上で2次関数
 ・・・(2)
・・・(2) が正定値の時,
が正定値の時,  である.)
である.) に対応する残差ベクトル
に対応する残差ベクトル は
は
 ・・・(3)
・・・(3) ・・・(4)
・・・(4) は単調に減少する.
ここで,
は単調に減少する.
ここで,  (最大固有値)/(最小固有値)であるとする.
ただし, 一般に収束判定に用いられる残差ノルム
(最大固有値)/(最小固有値)であるとする.
ただし, 一般に収束判定に用いられる残差ノルム は単調減少しない点に注意する.
は単調減少しない点に注意する.準備中














準備中
準備中
[10] Magnes R. Hestenes and Eduard Stiefel, Methods of conjugate gradients for solving linear systems, Journal of Research of the National Bureau of Standards 1952; 49(6):409–436.
[2] Richard Barrett, Michael W. Berry, Tony F. Chan, James Demmel, June Donato, Jack Dongarra,
Victor Eijkhout, Roldan Pozo, Charles Romine and Henk A. van der Vorst, Templates for the
Solution of Linear Systems: Building Blocks for Iterative Methods, SIAM: Philadelphia, PA,
1993.
P14–17
[14] Yousef Saad, Iterative Methods for Sparse Linear Systems, 2nd ed., SIAM: Philadelphia, PA,
2003.
P187–194
[27] Henk A. van der Vorst, Iterative Krylov Methods for Large Linear Systems, Cambridge University
Press: New York, NY, 2003.
P37–47
[23] Masaaki Sugihara and Kazuo Murota, Theoretical Numerical Linear Algebra, Iwanami Press:
Tokyo, 2009, (in Japanese).
P148–153
[29] 藤野 清次, 張 紹良, 反復法の数理 (応用数値計算ライブラリ) 朝倉書店, 1996.
P31–35