固有値問題解法の事例

固有値問題解法の事例 †

複素回転法による原子核多体共鳴状態の解析 †

提供: 理化学研究所仁科加速器研究センター 船木靖郎 (JICFuS), 2013年6月17日

共鳴状態を量子力学的に議論する際、共鳴の境界条件を付ける必要があるが、3体系以上の 多体共鳴に対して、正しい共鳴の境界条件は自明でない。そのような多体共鳴に対しても 適用可能な強力な方法に、複素回転法(Complex Scaling Method)がある。 この方法のメリットは、単に

(複素回転)

の変換を施すことで、正エネルギーの領域に対しても束縛状態同様の扱いで、共鳴パラメータ を決定できる点にある[1,2]。現在では、複素回転法は単に 共鳴パラメータを決定するだけでなく、核反応を含め共鳴状態の関与する様々な物理現象に 適用されその応用範囲を広げている[3]。

複素回転法では、複素回転されたハミルトニアン行列、Hに対し、次の一般化固有値問題を解くことが必要となる。

ここでHは複素対称(tH=H)、ノルム行列Nは実対称行列(tN=N) 上記一般化固有値問題は、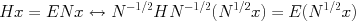

の形に変形でき、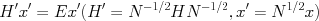

の標準固有値問題の形に帰着できる。この場合、まずNを対角化したうえで行列 H' を作り、 それを対角化するという手順を踏む。

既存のライブラリには、複素対称(密)行列に特化したサブルーチンは含まれていない ことが普通であり、まして数万次元程度の大規模並列計算用のものは皆無である。 今回、複素対称(密)行列に対する標準固有値問題を解き、全ての固有値、 固有ベクトルを求める並列計算用サブルーチンを開発した(PZDIAG)。

• 数値計算の道具箱：固有値問題の解法
• MPI 対応の複素対称行列対角化プログラム (JICFuS プロダクツ)
  

参考文献
[1] J. Aguilar and J. M. Combes, Commun. Math. Phys. 22, 269 (1971).
[2] E. Balslev and J. M. Combes, Commun. Math. Phys. 22, 280 (1971).
[3] H. Horiuchi, K. Ikeda and K. Kato, Prog. Theor. Phys. Suppl. No. 192, (Sec.7) (2012), and references therein.